Oblicz miarę kąta nachylenia ściany bocznej do podstawy wiedząc, że narysowany ostrosłup jest prawidłowy.
Oblicz wysokość ściany bocznej. Ściana boczna jest trójkątem równoramiennym, więc możesz wykorzystać twierdzenie Pitagorasa:
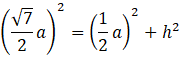
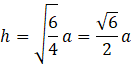
Odległość spodka wysokości ściany bocznej od spodka wysokości bryły ma długość równą wysokości trójkąta równobocznego o boku długości 𝑎, czyli ![]()
Oblicz miarę kąta, wykorzystując definicję funkcji trygonometrycznych:
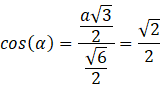
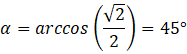
Odp. Ściana boczna jest nachylona do podstawy pod kątem 45°.

Oblicz długość wysokości ściany bocznej oraz odcinka łączącego spodek wysokości ściany bocznej oraz spodek wysokości bryły. Oba te odcinki to kolejno przeciwprostokątna oraz przyprostokątna przyległa do poszukiwanej miary kąta trójkąta prostokątnego. Wykorzystaj cosinus kąta, by uzależnić miarę kąta od długości krawędzi w ostrosłupie. Obliczamy wartość funkcji odwrotnej do cosinusa. Skorzystaj z tablic wartości funkcji trygonometrycznych lub kalkulatora.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
