Oblicz pole przekroju wiedząc, że dana bryła to sześcian.
Figura utworzona z przekroju jest równoległobokiem. Oblicz długości boków tego przekroju.
Dłuższy bok ma długość:
![]()
Krótszy bok ma długość:
![]()
Przekrój zawiera przekątną sześcianu o długości ![]()
Wykorzystaj twierdzenie cosinusów, by obliczyć cosinus kąta rozwartego równoległoboku:
![]()
![]()
![]()
Wykorzystaj jedynkę trygonometryczną, by wyznaczyć sinus tego kąta:
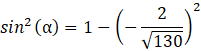
![]()
Kąt ![]()
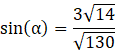
Oblicz pole równoległoboku:
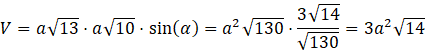

Zauważ, że przekrój jest równoległobokiem. Oblicz długości boków figury oraz zauważ, że dłuższa przekątna przekroju pokrywa się z przekątną sześcianu. Wykorzystaj twierdzenie cosinusów oraz jedynkę trygonometryczną, aby wyznaczyć sinus kąta między bokami równoległoboku. Oblicz pole, wykorzystując obliczone wartości.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
