Oblicz pole przekroju danego na siatce sześcianu.
Złóż bryłę z przedstawionej siatki:
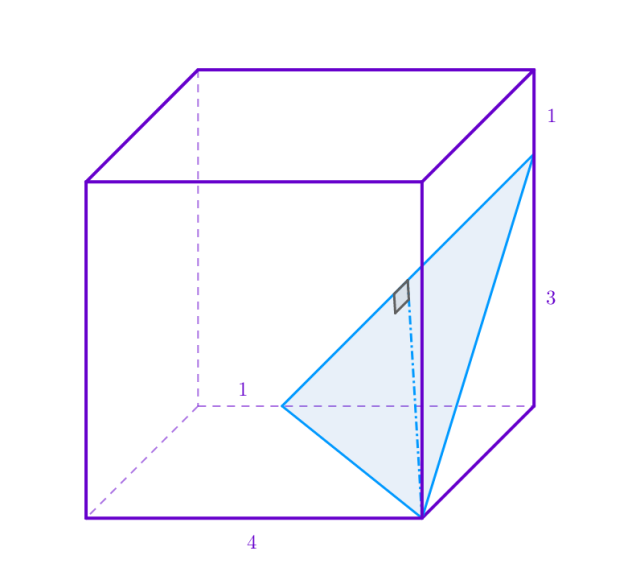
Przekrój bryły jest trójkątem równoramiennym. Długość ramion oraz podstawy możesz obliczyć za pomocą twierdzenia Pitagorasa:
![]()
![]()
Opuść wysokość na podstawę przekroju. Spodek wysokości dzieli podstawę na dwa odcinki o równej długości, a sama wysokość dzieli trójkąt na dwa przystające trójkąty prostokątne. Oblicz wysokość trójkąta, wykorzystując twierdzenie Pitagorasa:
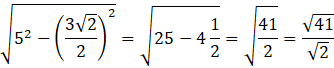
Pole przekroju jest równe:
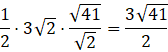

Złóż siatkę sześcianu i zidentyfikuj kształt przekroju bryły. Oblicz długość boków oraz wysokość przekroju za pomocą twierdzenia Pitagorasa. Oblicz pole przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
