Dany jest sześcian o krawędzi 𝑎, do którego doklejono identyczne ostrosłupy prawidłowe czworokątne na każdej ze ścian. Wyznacz wysokość tych ostrosłupów, dla których otrzymana bryła ma dwanaście ścian.
Zauważ, że aby bryła miała dwanaście ścian, sąsiadujące ściany boczne ostrosłupów muszą znajdować się na jednej płaszczyźnie i tworzyć romb:
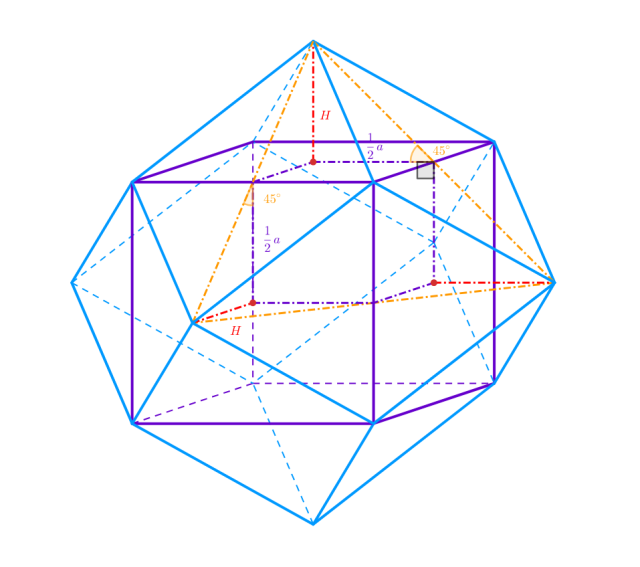
Wykorzystaj definicję funkcji trygonometrycznych, by obliczyć 𝐻:
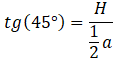
![]()
Odp. Wysokość ostrosłupów musi być równa ![]()

Zauważ, że ściany ostrosłupa muszą znajdować się na wspólnej płaszczyźnie, a następnie wykorzystaj definicję funkcji trygonometrycznych w trójkącie, by uzależnić wysokość ostrosłupa od długości krawędzi sześcianu.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
