Dany jest ostrosłup prosty o podstawie z trójkąta równoramiennego. Ramiona podstawy mają długość 6, natomiast podstawa – 4. Wiadomo też, że długość krawędzi bocznej jest równa 8. Oblicz miary kątów dwuściennych między ścianami bocznymi a płaszczyzną podstawy.
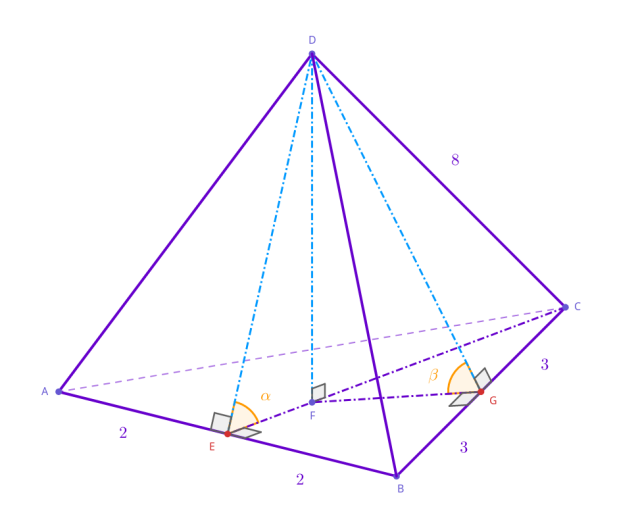
Oblicz długości odcinków 𝐶𝐸 oraz 𝐷𝐸 za pomocą twierdzenia Pitagorasa:
![]()
![]()
![]()
![]()
![]()
![]()
Skorzystaj z twierdzenia cosinusów, by obliczyć kąt α:
![]()
![]()
![]()
![]()
Oblicz wysokość ściany bocznej 𝐷𝐺:
![]()
![]()
Zauważ, że trójkąt 𝐶𝐹𝐺 jest podobny do trójkąta 𝐵𝐶𝐸 z cechy kkk. Wykorzystaj proporcje między podobnymi odcinkami, żeby obliczyć długość odcinka 𝐹𝐺:
![]()
![]()
![]()
Wykorzystaj definicję cosinusa, żeby obliczyć miarę kąta β:
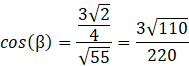
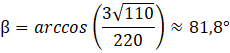
Odp. Ściany boczne nachylone są do płaszczyzny podstawy pod kątami około 71°, 82°, 82°.

Zauważ, że kąt α jest rozwarty na wysokościach dwóch ścian ostrosłupa. Oblicz ich długości, a następnie wykorzystaj twierdzenie cosinusów, by obliczyć ten kąt. Wiemy, że w ostrosłupie prostym spodek wysokości to również środek okręgu wpisanego podstawy. Pozwala to poprowadzić odcinek 𝐹𝐺 w taki sposób, że spotyka się w jednym punkcie z wysokością ściany bocznej. Oblicz długość obu tych odcinków za pomocą twierdzenia Pitagorasa oraz podobieństwa figur, a następnie skorzystaj z definicji cosinusa, żeby obliczyć kąt β. Skorzystaj z tablicy wartości funkcji trygonometrycznych lub kalkulatora.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
