Dany jest graniastosłup prawidłowy ośmiokątny o krawędzi podstawy 𝑎 i krawędzi bocznej 𝑏. Oblicz stosunek 𝑏 do 𝑎, dla którego najdłuższa przekątna tego graniastosłupa jest nachylona pod kątem 45° do podstawy.
Rzut najdłuższej przekątnej graniastosłupa prawidłowego ośmiokątnego na podstawę tworzy najdłuższą przekątną podstawy. By móc wyliczyć poszukiwany stosunek, będziesz musiał obliczyć długość tej przekątnej. Oznacz ją jako 𝑑.
Zaznacz wszystkie przekątne ośmiokąta foremnego, które przechodzą przez jego środek. Zauważ, że te przekątne tworzą osiem trójkątów równoramiennych. Podwojona długość ramienia tego trójkąta to długość poszukiwanej przekątnej.
Kąt między ramionami jednego z tych trójkątów ma miarę:
![]()
Ze środka ośmiokąta opuść wysokość na podstawę trójkąta. Dzieli ona podstawę na dwie równe części oraz jest dwusieczną kąta między ramionami. Wykorzystaj funkcje trygonometryczne, by uzależnić długość przekątnej podstawy graniastosłupa od długości krawędzi podstawy:
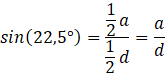
Nie znasz dokładnej wartości sinusa dla takiego kąta, ale jesteś w stanie ją obliczyć. Przekształć wzór na cosinus podwojonego kąta:
![]()
![]()
![]()
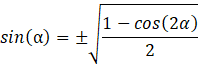
Obliczany kąt należy do przedziału ![]()
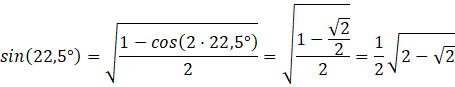
Obliczamy długość 𝑑:
![]()
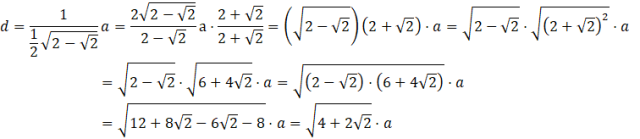
Chcemy, żeby przekątna graniastosłupa była nachylona pod kątem ![]()
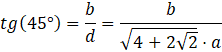
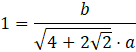
![]()
Odp. Stosunek krawędzi bocznej do krawędzi podstawy powinien wynosić ![]()

Wykorzystaj regularność wielokątów foremnych, żeby uzależnić długość przekątnej podstawy od długości krawędzi. Zauważ, że jesteś w stanie wyliczyć dokładną wartość funkcji trygonometrycznych dla połowy kąta o znanej wartości, przekształcając wzory na funkcje trygonometryczne podwojonego kąta. Uprość wyrażenie niewymierne, a następnie wykorzystaj definicję funkcji trygonometrycznych, by znaleźć stosunek odpowiednich krawędzi.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
