Dany jest ostrosłup przedstawiony na rysunku. Odcinek pokolorowany na zielono to wysokość ostrosłupa. Pole podstawy wynosi 𝑃, natomiast zaznaczona krawędź podstawy ma długość 𝑎. Wskaż wzór na objętość tego ostrosłupa:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Oblicz wysokość podstawy:
![]()
![]()
Wysokość dzieli trójkąt zawierający kąty α oraz β na dwa trójkąty prostokątne o wspólnej przyprostokątnej będącej wysokością bryły. Ustaw jako niewiadomą 𝑥 długość odcinka od wierzchołka przy kącie α do spodka wysokości bryły. Ułóż układ równań za pomocą funkcji trygonometrycznych:
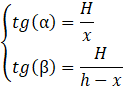
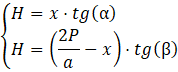
Otrzymasz równanie:
![]()
z którego wyznaczysz zmienną ![]()
![]()
![]()
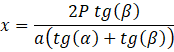
Wysokość 𝐻 jest równa:
![]()
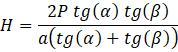
Oblicz objętość ostrosłupa:
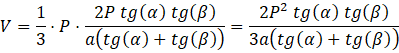
Odp. D. ![]()

Oblicz wysokość opuszczoną na krawędź 𝑑 względem jej długości oraz pola podstawy. Następnie ułóż układ równań z pomocą definicji funkcji trygonometrycznych, by uzależnić wysokość ostrosłupa od danych w zadaniu. Oblicz wysokość bryły i porównaj ze zbiorem odpowiedzi.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
