Dany jest graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 𝑎wraz z zacieniowanym przekrojem, przedstawionym na rysunku. Oblicz pole tego przekroju.
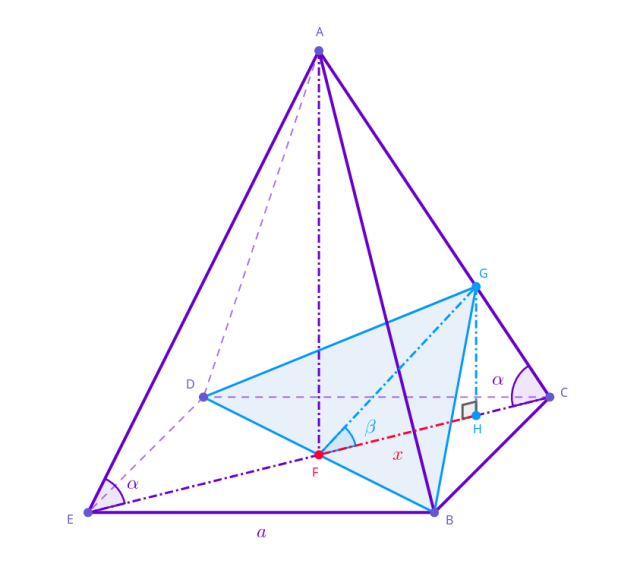
Odcinek 𝐹𝐶 ma długość połowy przekątnej podstawy, czyli ![]()
Długość odcinka 𝐺𝐻 można opisać na dwa sposoby:
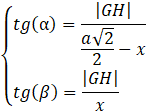
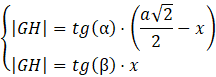
Przyrównaj prawe strony równań, żeby wyznaczyć 𝑥:
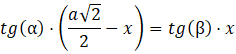
![]()
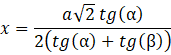
Długość odcinka 𝐺𝐻 wynosi więc:
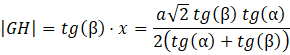
Oblicz długość odcinka 𝐺𝐹 za pomocą twierdzenia Pitagorasa:
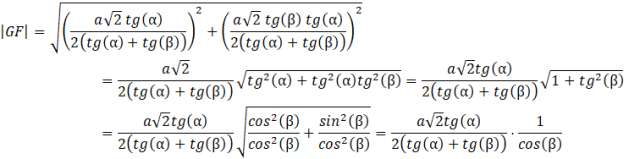
Uprość sumę ![]()
![]()
Kontynuuj upraszczanie wyrażenia:
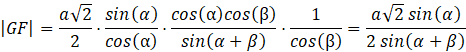
Pole przekroju jest równe:
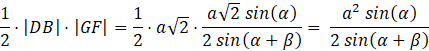

Zauważ, że wysokość przekroju jest oparta o odcinek 𝐺𝐻. Opisz długość odcinka 𝐺𝐻 na dwa sposoby za pomocą funkcji trygonometrycznych kąta α i β. Oblicz długość odcinka 𝐹𝐻 oraz 𝐺𝐻 i wykorzystaj twierdzenie Pitagorasa, by obliczyć odcinek 𝐹𝐺. Uprość sumę tangensów, pamiętając wzór na sinus sumy kątów. Oblicz pole przekroju za pomocą wzoru na pole trójkąta.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
