Oblicz obwód zacieniowanego przekroju wiedząc, że ostrosłup na rysunku jest prawidłowy.
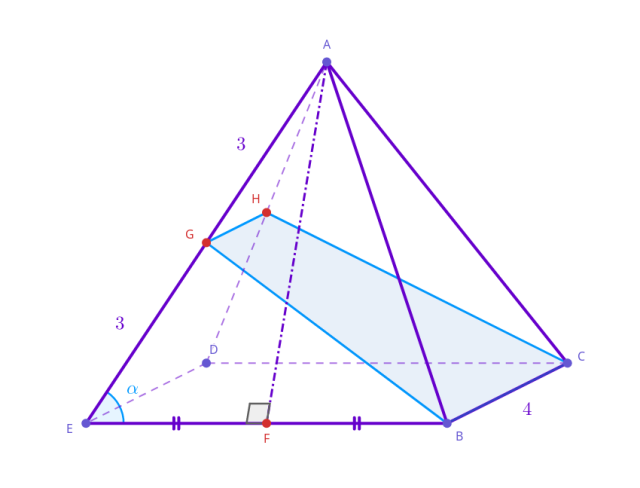
Odcinek 𝐺𝐻 to linia środkowa ściany bocznej 𝐴𝐷𝐸. Wobec tego jego długość wynosi połowę długości podstawy, czyli 2.
Opuść wysokość 𝐴𝐹 na podstawę 𝐵𝐸 w ścianie bocznej ostrosłupa. Ta ściana jest trójkątem równoramiennym, więc spodek wysokości 𝐹 dzieli podstawę na dwie równe części. Oblicz cosinus kąta α za pomocą definicji funkcji trygonometrycznych:
![]()
Oblicz długość odcinka 𝐵𝐺 za pomocą twierdzenia cosinusów:
![]()
![]()
![]()
![]()
Długość |𝐶𝐻| jest identyczna, ponieważ trójkąty 𝐵𝐸𝐺 i 𝐶𝐷𝐻 są przystające z cechy bkb.
Obwód przekroju jest równy:
![]()

Wykorzystaj relacje między odcinkami charakterystycznymi w trójkątach równoramiennych oraz definicje funkcji trygonometrycznych, aby obliczyć cosinus kąta przy podstawie ściany bocznej. Oblicz długość boku przekroju za pomocą twierdzenia cosinusów. Zsumuj długości boków przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
