Dany jest graniastosłup prosty o podstawie rombu. Kąty nachylenia przekątnych bryły do podstawy wynoszą odpowiednio 45° i 60°. Oblicz kąt nachylenia ścian w tym graniastosłupie.
Trójkąty prostokątne utworzone przez przekątne graniastosłupa tworzą charakterystyczne trójkąty prostokątne (![]()
![]()
![]()
Wykorzystaj fakt, że przekątne rombu przecinają się pod kątem prostym, oraz że punkt przecięcia się przekątnych dzieli te przekątne na dwie równe części. Oblicz miarę jednego z kątów trójkąta prostokątnego utworzonego przez przekątne podstawy, który jest połową miary kąta jednego z kątów wewnętrznych rombu:
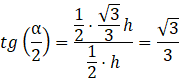

Kąty przy jednym z boków równoległoboku sumują się do 180°, więc:
![]()
Odp. Miary kątów między ścianami wynoszą ![]()

Wykorzystaj konstrukcję graniastosłupa i dane podane w treści zadania, by wyznaczyć długości przekątnych podstawy. Zauważ, że przekątne dzielą romb na cztery przystające trójkąty prostokątne i oblicz miarę kąta wewnętrznego przy przeciwprostokątnej jednego z tych trójkątów za pomocą funkcji trygonometrycznych. Skorzystaj z tablic wartości funkcji trygonometrycznych lub kalkulatora.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
