Dany jest czworościan foremny przedstawiony na rysunku. Oblicz pole zacieniowanego przekroju.
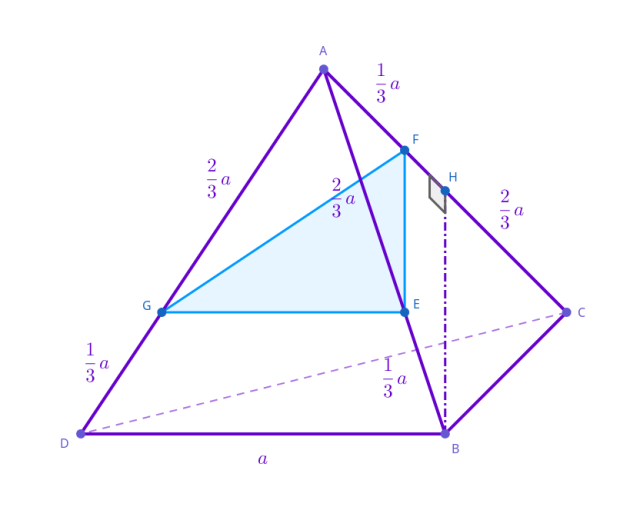
Zauważ, że trójkąty 𝐴𝐷𝐵 i 𝐴𝐺𝐸 są podobne z cechy bkb. Oblicz skalę podobieństwa:
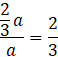
Oznacza to, że odcinek 𝐺𝐸 ma długość:
![]()
Trójkąty 𝐴𝐹𝐺 i 𝐴𝐹𝐸 są przystające, czyli przekrój to trójkąt równoramienny.
Trójkąty 𝐴𝐹𝐸 i 𝐴𝐵𝐻 są podobne z cechy bkb. Oblicz skalę podobieństwa:
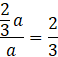
Oznacza to, że odcinek 𝐸𝐹 oraz odcinek 𝐹𝐺 mają długości:
![]()
Opuść wysokość na bok 𝐺𝐸 trójkąta 𝐸𝐹𝐺. Spodek tej wysokości dzieli podstawę na dwa równe odcinki. Oblicz wysokość za pomocą twierdzenia Pitagorasa:
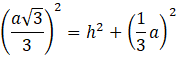
![]()
![]()
Oblicz pole przekroju:
![]()

Wykorzystaj podobieństwa trójkątów utworzonych przez krawędzie przekrojów w ścianach bocznych, by wyznaczyć ich długości. Oblicz wysokość przekroju za pomocą twierdzenia Pitagorasa. Oblicz pole przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
