Dany jest sześcian o krawędzi 𝑎oraz jego przekrój przedstawiony na rysunku. Płaszczyzna przekroju jest nachylona pod kątem α do płaszczyzny podstawy. Oblicz pole przekroju.
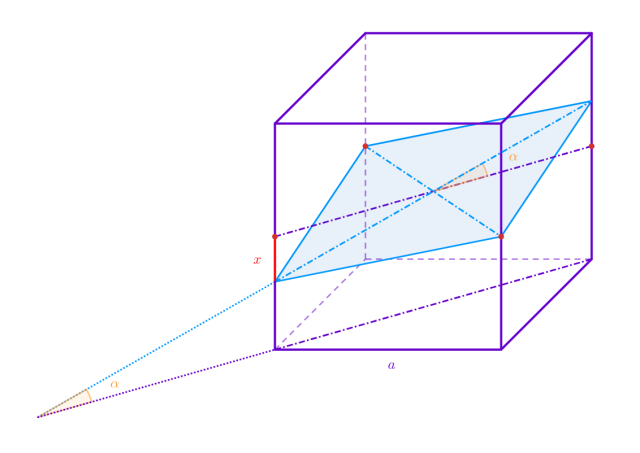
Przekrój przedstawiony w zadaniu jest rombem. Aby wyznaczyć wzór na pole przekroju, oblicz długości przekątnych tego przekroju.
Krótsza przekątna ma długość równą przekątnej podstawy, czyli ![]()
Długość dłuższej przekątnej zależy od kąta nachylenia ![]()
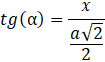
![]()
Oblicz długość dłuższej przekątnej przekroju za pomocą twierdzenia Pitagorasa:
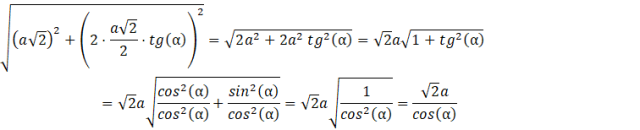
Pole przekroju wynosi:
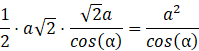

Rozpoznaj w przekroju bryły romb. Oblicz długości jego przekątnych i wylicz pole. Skorzystaj przy tym z definicji funkcji trygonometrycznych, twierdzenia Pitagorasa oraz jedynki trygonometrycznej.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
