Spójrz na rysunek. Oblicz pole zacieniowanego przekroju wiedząc, że bryła na rysunku jest prawidłowa.
Zacieniowany przekrój jest trapezem. Podstawa zawarta w górnej podstawie graniastosłupa to przekątna kwadratu, czyli ma długość ![]()
Podstawa zawarta w dolnej podstawie graniastosłupa to przeciwprostokątna trójkąta prostokątnego równoramiennego o boku długości 5. Długość podstawy wynosi więc ![]()
Wysokość trapezu to przeciwprostokątna trójkąta prostokątnego opartego na przyprostokątnych z wysokości bryły oraz ![]()
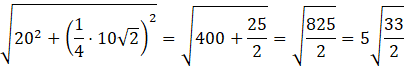
Pole przekroju wynosi:
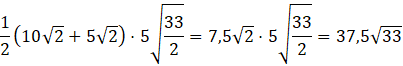

Wysokość przekroju obliczasz za pomocą twierdzenia Pitagorasa. Zauważ, że odcinek łączący środek podstawy (będący jednocześnie spodkiem wysokości) prostopadle z krótszą podstawą przekroju tworzy przyprostokątną trójkąta prostokątnego. Długość tego odcinka wynosi jedną czwartą długości przekątnej, ponieważ trójkąt o przyprostokątnych 5 oraz trójkąt o przyprostokątnych 10 to trójkąty podobne skalą podobieństwa ![]()

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
