Udowodnij, że punkty styczności boków podstawy z okręgiem wpisanym są spodkami wysokości ścian bocznych ostrosłupa, zakładając, że spodek wysokości bryły jest środkiem okręgu wpisanego.
Z:
Środek okręgu wpisanego w podstawę jest spodkiem wysokości bryły.
T:
Punkty styczności okręgu wpisanego i boków podstawy to spodki wysokości ścian bocznych.
D:
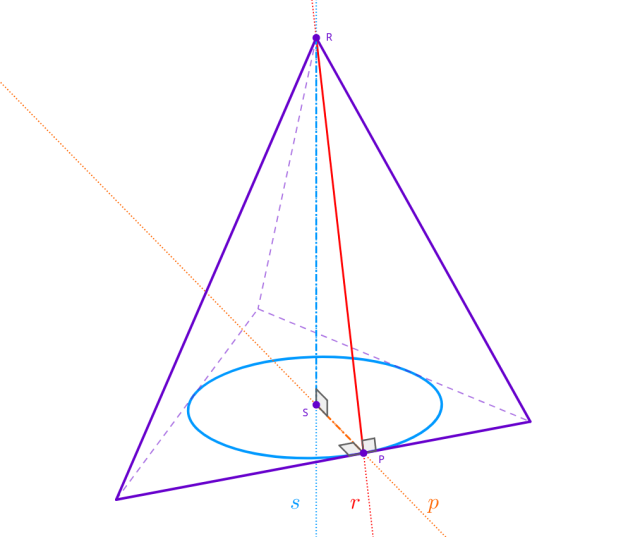
Prowadzimy prostą 𝑟 przez wierzchołek 𝑅 ostrosłupa, prostopadłą do podstawy ściany. Do prostej należy wysokość ściany bocznej 𝑃𝑅, gdzie 𝑃 to spodek wysokości. Rzutujemy prostokątnie prostą 𝑟 na płaszczyznę podstawy. Z definicji rzutu prostokątnego, tworzymy prostą 𝑠 prostopadłą do płaszczyzny podstawy, przechodzącą przez punkt 𝑅. Oznacza to, że prosta 𝑠 musi zawierać wysokość ostrosłupa opuszczoną na podstawę ze wpisanym okręgiem. Z założenia wiemy, że środek okręgu wpisanego w podstawę jest spodkiem wysokości ostrosłupa, to znaczy, że rzutem prostokątnym wierzchołka 𝑅 na płaszczyznę podstawy jest 𝑆, środek okręgu wpisanego.
Z twierdzenia o trzech prostych prostopadłych mamy, że prosta 𝑝 będąca rzutem prostej 𝑟 na płaszczyznę podstawy jest prostopadła do krawędzi podstawy zawierającej punkt 𝑃.
Prosta 𝑝 jest prostopadła do krawędzi podstawy oraz zawiera środek okręgu wpisanego w trójkąt. Oznacza to, że prosta ta zawiera punkt styczności i jest to punkt przecięcia się krawędzi podstawy z prostą 𝑝.
Zauważamy, że proste 𝑝, 𝑟 oraz krawędź podstawy przecinają się w jednym punkcie, który jest punktem styczności okręgu wpisanego oraz spodkiem wysokości ściany bocznej. ![]()

Wykorzystaj rzut prostokątny prostej zawierającej wysokość ściany bocznej na podstawę, by pokazać, że spodek wysokości i punkt styczności okręgu wpisanego to jeden i ten sam punkt.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
