Udowodnij, że wzór na objętość ostrosłupa ściętego ma postać ![]()
Teza:
Objętość ostrosłupa ściętego o danej wysokości i polach podstaw wyraża się wzorem:
![]()
Dowód:
Niech dany będzie pewien ostrosłup ścięty, o wysokości ![]()
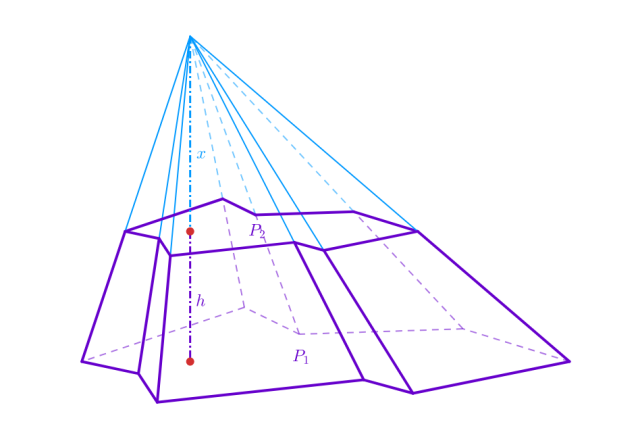
Dopełnij ostrosłup ścięty do pełnego ostrosłupa. Ostrosłup o podstawie z figury o polu 𝑃₂ jest podobny do ostrosłupa o podstawie z figury o polu 𝑃₁ . Skalę podobieństwa między tymi bryłami można zapisać na następujące sposoby:
![]()
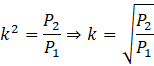
Uzależnij długość 𝑥 od parametrów ostrosłupa ściętego poprzez przyrównanie prawych stron równań:
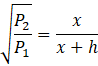
![]()
![]()
![]()
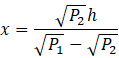
Objętości: całego ostrosłupa oraz mniejszego ostrosłupa podobnego wynoszą kolejno:
![]()
![]()
Objętość ostrosłupa ściętego jest równa różnicy tych dwóch objętości:
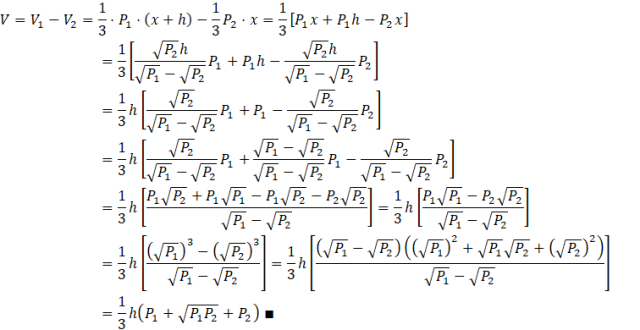

Dopełnij ostrosłup ścięty do pełnego ostrosłupa. Otrzymasz wtedy mniejszy ostrosłup, podobny do całości bryły. Uzależnij wysokość mniejszego, dopisanego ostrosłupa od pozostałych parametrów, zapisując skalę podobieństwa między ostrosłupami podobnymi na dwa różne sposoby. Zapisz symbolicznie objętości podobnych ostrosłupów – różnica tych wyrażeń to poszukiwana objętość ostrosłupa ściętego. Wykorzystaj obliczoną wartość wysokości mniejszego ostrosłupa oraz wzór na różnicę sześcianów:
![]()
żeby uprościć wyrażenie i otrzymać oczekiwaną formę.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
