Ostrosłupy na rysunkach są prawidłowe. Oblicz pola zaznaczonych w nich przekrojów.
Porównaj trójkąty o przeciwprostokątnej z przekątnej podstawy i przeciwprostokątnej z podstawy przekroju. Zauważ, że są to trójkąty podobne w skali ![]()
Długość podstawy przekroju wynosi ![]()
Oblicz wysokość bryły z twierdzenia Pitagorasa, zauważając trójkąt prostokątny o przeciwprostokątnej z krawędzi bocznej ostrosłupa oraz przyprostokątnych z połowy przekątnej podstawy oraz wysokości bryły:
![]()
![]()
![]()
Znasz skalę podobieństwa, więc zauważ, że podstawa przekroju dzieli połowę przekątnej podstawy na dwa równe odcinki. Jeden z tych odcinków wraz z wysokością bryły tworzy trójkąt prostokątny o przeciwprostokątnej z wysokości przekroju. Skorzystaj z twierdzenia Pitagorasa:
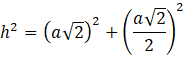
![]()
![]()
Pole przekroju wynosi:
![]()

Oblicz długość podstawy przekroju. Zauważ podobieństwo trójkątów w podstawie ostrosłupa. Wykorzystaj skalę, by obliczyć przyprostokątną zawartą w podstawie, na której oparta jest przeciwprostokątna będąca wysokością przekroju. Wykorzystaj twierdzenie Pitagorasa, żeby obliczyć tę wysokość. Oblicz pole przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
