Dany jest pewien graniastosłup prosty o podstawie z trójkąta równoramiennego. Charakteryzuje się on tym, że przekątne jego ścian bocznych są nachylone do płaszczyzny podstawy pod kątami odpowiednio 45° i 60°. Wyznacz miarę kąta dwuściennego tworzonego przez ściany boczne graniastosłupa. Rozważ dwa przypadki.
Oznacz długość krawędzi bocznej jako 𝘩. Podstawę podstawy graniastosłupa oznacz jako 𝑎, natomiast ramiona jako 𝑏. Zauważ, że przekątne ścian bocznych stanowią przeciwprostokątne trójkątów prostokątnych. Skorzystaj z definicji funkcji trygonometrycznych, żeby uzależnić długość krawędzi podstawy od wysokości:
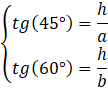
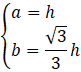
Opuść wysokość trójkąta równoramiennego na podstawę. Spodek wysokości dzieli podstawę 𝑎 na dwa odcinki równej długości. Wykorzystaj funkcje trygonometryczne, żeby obliczyć kąt przy ramieniu trójkąta:
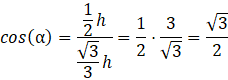
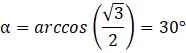
Czyli kąty wewnętrzne podstawy trójkąta to 30°, 30°, 120°. Graniastosłup jest prosty, czyli są to również kąty między ścianami bocznymi.
Drugi przypadek mamy, gdy rozważymy inne kąty przy przekątnych ścian bocznych:
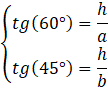
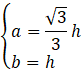
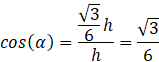
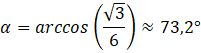
Czyli kąty wewnętrzne podstawy trójkąta w tym przypadku wynoszą około 73°, 73°, 34°.

Oznacz krawędzi w graniastosłupie. Wykorzystaj funkcje trygonometryczne, by uzależnić odpowiednie wartości od siebie. Wykorzystaj je ponownie w trójkącie prostokątnym utworzonym przez wysokość opuszczoną na podstawę trójkąta równoramiennego. Podaj miarę kąta, korzystając z tablicy wartości funkcji trygonometrycznych lub z kalkulatora.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
