Dany jest sześcian o długości 𝑎. Podzielono go na dwie bryły za pomocą płaszczyzny przechodzącej przez trzy wierzchołki sześcianu, nienależące do tylko jednej ściany. Oblicz pola powierzchni oraz objętości tych brył.
Jedna z otrzymanych brył to ostrosłup o podstawie z trójkąta prostokątnego o przyprostokątnej długości 𝑎 oraz wysokości tej samej długości. Objętość zacieniowanej bryły wynosi:
![]()
Objętość drugiej bryły to:
![]()
Pole powierzchni pierwszej bryły to trzy ściany zbudowane z połowy ściany bocznej sześcianu oraz trójkąta równobocznego o krawędzi równej przekątnej ściany bocznej:
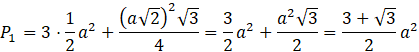
Pole powierzchni drugiej bryły to pole trzech ścian bocznych, trzech połówek kwadratu oraz trójkąta równobocznego:
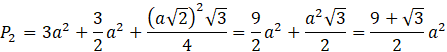

Zidentyfikuj kształt brył oraz kształt figur stanowiących ściany boczne. Oblicz objętości i pola powierzchni, znając długość krawędzi sześcianu.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
