Dany jest ostrosłup prawidłowy czworokątny o długości krawędzi podstawy 10 i wysokości 12. Do ostrosłupa wpisano kulę, po czym wpisano kolejna, mniejszą kulę w taki sposób, że kule są ze sobą styczne oraz mniejsza kula jest styczna do czterech ścian bocznych ostrosłupa. Oblicz promienie kul.
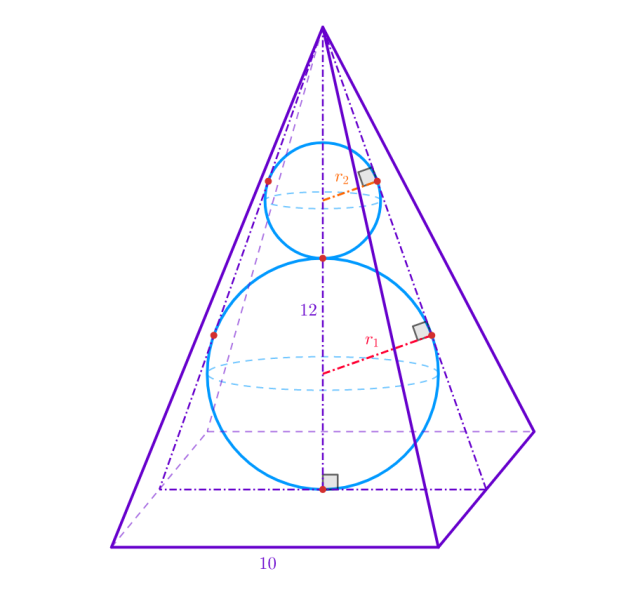
Oblicz wysokość ściany bocznej ostrosłupa:
![]()
![]()
Zauważ, że trójkąty prostokątne wyznaczone przez: odcinek łączący środek podstawy z krawędzią, promień większej kuli oraz promień mniejszej kuli, są podobne (kąt – kąt – kąt). Wykorzystaj proporcje odpowiednich odcinków, by wyliczyć promienie kul:
![]()
![]()
![]()
![]()
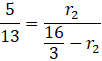
![]()
![]()
Odp. Promienie wpisanych kul to kolejno: ![]()
![]()

Wykorzystaj twierdzenie Pitagorasa, by obliczyć niewiadomą wysokość ściany bocznej (można też zauważyć, że jest to trójka pitagorejska) oraz podobieństwo trójkątów utworzonych przez wpisane kule.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
