Dany jest ostrosłup prawidłowy czworokątny o długości krawędzi podstawy równej 6. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 30°. Oblicz miarę kąta dwuściennego między ścianą boczną a płaszczyzną podstawy tego ostrosłupa.
Zauważ, że kąt utworzony przez krawędź boczną jest zawarty w trójkącie prostokątnym utworzonym przez połowę przekątnej podstawy ostrosłupa oraz jego wysokość. Oznacz tą wysokość jako 𝐻. Skorzystaj z tangensa kąta, by obliczyć wysokość ostrosłupa:
![]()
![]()
Poprowadź odcinek ze spodka wysokości prostopadle do krawędzi podstawy. Jest to przyprostokątna trójkąta prostokątnego, którego kąt przy przeciwprostokątnej to poszukiwany kąt. Wykorzystaj definicję tangensa kąta, żeby obliczyć miarę tego kąta:
![]()
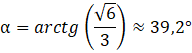
Odp. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem około 39°.

Wykorzystaj funkcje trygonometryczne, by obliczyć wysokość ostrosłupa. Kąt nachylenia krawędzi do podstawy oraz kąt nachylenia ściany bocznej do podstawy zawierają się w trójkątach prostokątnych, którego przyprostokątną jest właśnie wysokość ostrosłupa. Skorzystaj z tablicy wartości funkcji trygonometrycznych lub z kalkulatora, żeby wyznaczyć miarę kąta.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
