Wyprowadź wzór ogólny na objętość stożka ściętego o wysokości 𝘩 i promieniach podstaw równych 𝑟 oraz 𝑅.
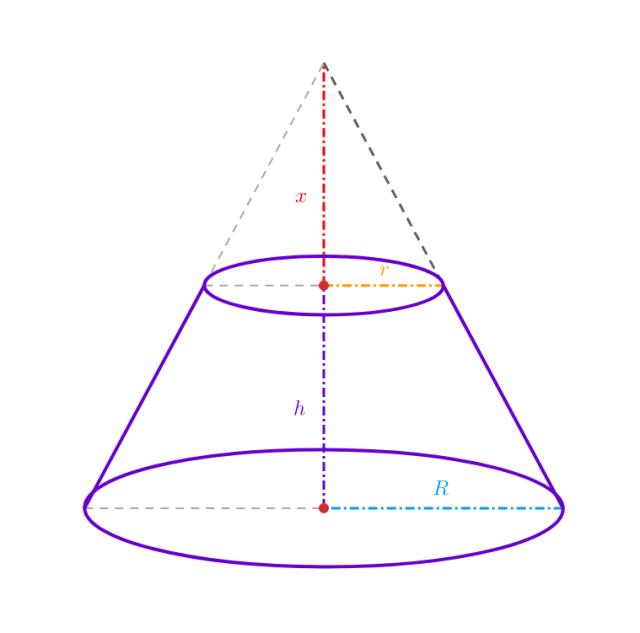
Doszkicuj stożek na mniejszej podstawie ściętego ostrosłupa w taki sposób, by był on podobny do całości utworzonego w ten sposób stożka. Zauważ, że krawędzie zawarte w płaszczyźnie zawierającej oś obrotu są do siebie podobne. Uzależnij długość krawędzi ![]()
![]()
![]()
![]()
![]()
Oblicz objętość ostrosłupa o podstawie z większej oraz mniejszej podstawy ostrosłupa ściętego:
![]()
![]()
Objętość stożka ściętego to różnica tych dwóch objętości:
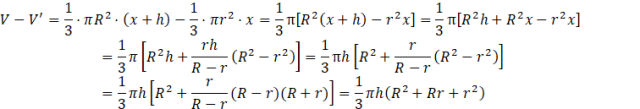

Wykorzystaj podobieństwo stożków utworzonych przez większą oraz mniejszą podstawę stożka ściętego, by uzależnić wysokość mniejszego ze stożków od zmiennych podanych w treści zadania. Oblicz objętości tych stożków, korzystając ze wzoru, a następnie oblicz i uprość powstałą różnicę.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
