Dany jest graniastosłup prawidłowy sześciokątny oraz zaznaczony w nim trójkąt w sposób przedstawiony na rysunku. Udowodnij, że jest to trójkąt prostokątny oraz oblicz miary jego kątów ostrych.
W treści zadania mamy, że jest to graniastosłup prawidłowy, czyli jego ściany są prostopadłe do płaszczyzny podstawy. Mamy w ten sposób gwarancję, że wysokość graniastosłupa jest prostopadła do krótszej przekątnej podstawy. Krótsza przekątna dzieli kąt wewnętrzny sześciokąta na kąty 90° i 30°. Oznacza to, że krótsza przekątna podstawy jest prostopadła do jej krawędzi. Krótsza przekątna podstawy jest prostopadła do dwóch przecinających się odcinków należących do płaszczyzny ściany bocznej, więc dowolna prosta należąca do tej płaszczyzny jest do tej przekątnej prostopadła. Odcinek należy do płaszczyzny oraz rozważanego trójkąta, więc trójkąt ten jest prostokątny. ![]()
Oblicz długości dwóch boków trójkąta. Długość boku zawartego w ścianie bocznej oblicz za pomocą twierdzenia Pitagorasa:
![]()
Długość krótszej przekątnej podstawy graniastosłupa to długość krawędzi podstawy razy ![]()
![]()
Oblicz miarę jednego z ostrych kątów za pomocą definicji funkcji trygonometrycznych:
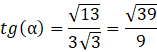
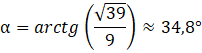
Miarę drugiego kąta wyliczysz, korzystając z sumy kątów wewnętrznych w trójkącie:
![]()
Odp. Kąty ostre w zaznaczonym trójkącie mają miary około 35° i 55°.

W dowodzie wykorzystaj twierdzenie, że jeżeli prosta jest prostopadła do dwóch przecinających się prostych, to jest prostopadła do każdej prostej leżącej na płaszczyźnie zawierającej te przecinające się proste.
W części obliczeniowej wykorzystaj konstrukcję oraz dane podane w zadaniu, by za pomocą twierdzenia Pitagorasa obliczyć długości dwóch boków zaznaczonego trójkąta. Wykorzystaj odpowiednie funkcje trygonometryczne, by znaleźć miarę jednego z ostrych kątów wewnętrznych trójkąta. Skorzystaj z tablic wartości funkcji trygonometrycznych lub kalkulatora.
Krótsza przekątna podstawy krawędzie graniastosłupa prawidłowego sześciokątnego ma długość ![]()

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
