Dany jest prostopadłościan o wymiarach 3 cm ⨉ 4 cm ⨉ 4 cm. Znajdź przekrój w kształcie trójkąta o największym polu i oblicz jego pole.
Żeby płaszczyzna przecinająca prostopadłościan utworzyła trójkąt, musi ona zawierać punkty należące do trzech krawędzi wychodzących z jednego wierzchołka bryły. Zauważ następujący przekrój prostopadłościanu:
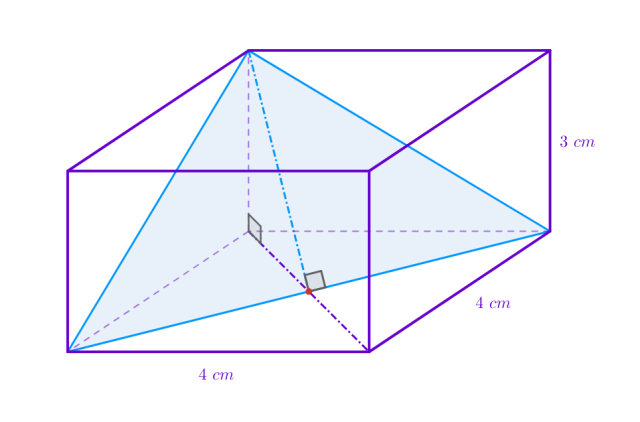
Długość podstawy tego trójkąta jest równa długości przekątnej podstawy, czyli ma długość ![]()
![]()
Pole przekroju wynosi:
![]()

Ze względu na to, że poszukujemy przekrojów trójkątnych o maksymalnym polu, interesują cię przekroje składające się z trzech przekątnych ścian prostopadłościanu. Oblicz długość podstawy oraz wysokość przekroju i wykorzystaj je do obliczenia pola.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
