Dany jest czworościan foremny o krawędzi 𝑎, w którym zawarty jest kolejny czworościan foremny w taki sposób, że środki ścian bocznych większego czworościanu są jego wierzchołkami. Oblicz długość krawędzi mniejszego czworościanu.
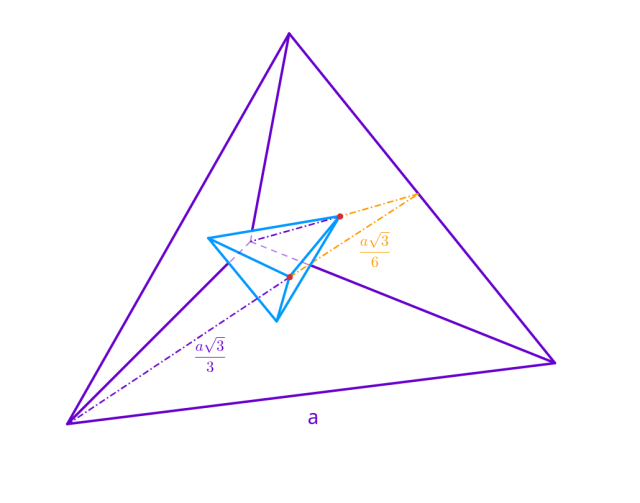
Zauważ, że wierzchołki czworościanu zawierają się w wysokościach ścian większego czworościanu. Zaznacz trójkąt z dwóch wysokości ścian oraz krawędzi podstawy czworościanu. Wykorzystaj twierdzenie Talesa oraz fakt, że środek trójkąta równobocznego dzieli jego wysokość w stosunku 1 : 2 i oblicz długość krawędzi wpisanej bryły:
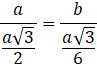
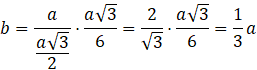
Odp. Krawędź mniejszego czworościanu ma długość ![]()

Zauważ, że wierzchołki czworościanu zawierają się w wysokościach ścian większego czworościanu i wyznacz długości trójkąta rozpiętego na tych wysokościach. Wykorzystaj twierdzenie Talesa lub podobieństwo figur, by wyznaczyć krawędź wpisanej bryły. Twierdzenie Talesa ma zastosowanie, ponieważ podział wysokości spełnia warunki twierdzenia odwrotnego do twierdzenia Talesa, czyli odpowiadające krawędzie są równoległe (alternatywnie wykorzystujemy podobieństwo figur z zasady – bkb).

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
