Dany jest graniastosłup prawidłowy sześciokątny. Jego krawędź podstawy ma długość 6, a wysokość 9. Oblicz pole przekroju zaznaczonego na rysunku.
Przekrój przedstawiony na rysunku jest trójkątem równoramiennym. Jego ramiona to przekątne ścian bocznych. Podstawa ma długość krótszej przekątnej podstawy. Zauważ, że krótsza przekątna podstawy dzieli dłuższą przekątną podstawy do niej prostopadłą w stosunku 3 : 1. Zauważ również, że wysokość przekroju opuszczona na podstawę to przeciwprostokątna trójkąta prostokątnego o przyprostokątnych z wysokości graniastosłupa i jednej czwartej dłuższej przekątnej podstawy. Pole przekroju wynosi więc:
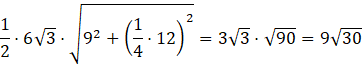

Z rysunku zauważ, że krótsza przekątna podstawy dzieli dłuższą przekątną podstawy do niej prostopadłą w stosunku 3 : 1, ponieważ krótsza przekątna to dwie wysokości trójkątów równobocznych, z których składa się sześciokąt foremny. Spodek wysokości dzieli podstawę trójkąta równobocznego na dwie równe części, więc dłuższa część przekątnej składa się z trzech połówek, a krótsza z jednej. Oblicz wysokość trójkąta, wykorzystując twierdzenie Pitagorasa. Oblicz pole przekroju.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
