Dany jest przekrój prostopadłościanu przedstawionego na rysunku. Oblicz największą miarę kąta wewnętrznego tego przekroju.
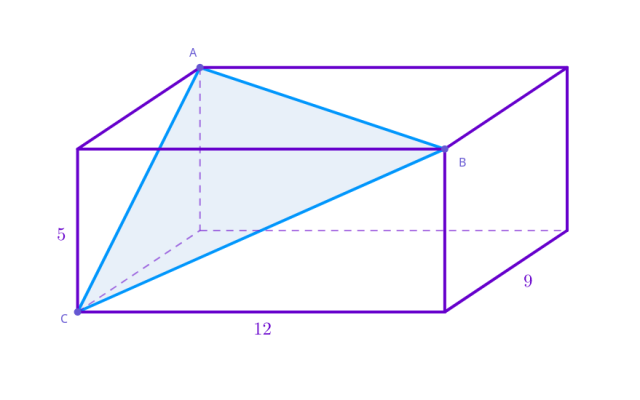
Oblicz długości odcinków 𝐴𝐵, 𝐴𝐶, 𝐵𝐶 za pomocą twierdzenia Pitagorasa:
![]()
![]()
![]()
![]()
![]()
![]()
Mamy, że |𝐴𝐵| > |𝐴𝐶| oraz |𝐴𝐵| > |𝐵𝐶|, więc największy kąt w przekroju to kąt ∢𝐴𝐶𝐵. Oblicz ten kąt, korzystając z twierdzenia cosinusów:
![]()
![]()
![]()
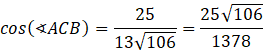
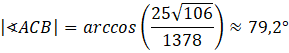

Oblicz długości boków przekroju, wykorzystując twierdzenie Pitagorasa. Największy kąt wewnętrzny jest rozpięty naprzeciwko najdłuższego boku. Skorzystaj z twierdzenia cosinusów, żeby wyznaczyć ten kąt. Miarę odczytaj, korzystając z tablic wartości trygonometrycznych lub kalkulatora.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
