Niech dany będzie ostrosłup prosty o podstawie prostokąta, którego boki mają długość 1 i ![]()
Naszkicuj sytuację przedstawioną w treści zadania:
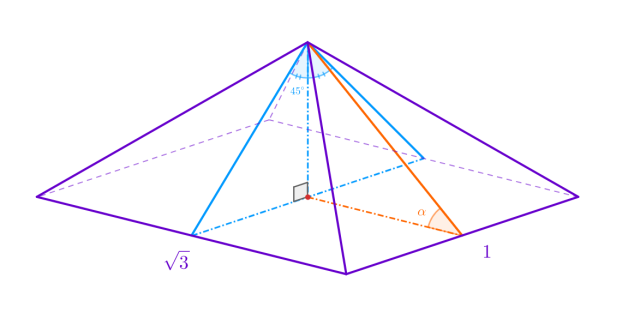
Płaszczyzna zawierająca kąt dwuścienny między większymi ścianami bocznymi tworzy w bryle niebieski trójkąt, zawierający wysokość bryły. Zauważ, że trójkąt prostokątny utworzony przez wysokość bryły ma kąty wewnętrzne 45°, 45°, 90°, czyli wysokość ostrosłupa jest równa połowie krótszej krawędzi podstawy - ![]()
![]()
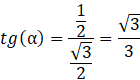
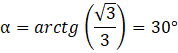
Odp. Mniejsze ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 30°.

Wyznacz płaszczyznę prostopadłą do większych ścian bocznych ostrosłupa w taki sposób, by zawierała ona wysokość ostrosłupa. Płaszczyzna ta wyznacza niebieski, prostokątny trójkąt równoramienny. Wysokość bryły dzieli ten trójkąt na dwa przystające równoramienne trójkąty prostokątne. Wykorzystaj zależności między bokami w tym trójkącie, by wyznaczyć wysokość bryły. Oblicz miarę kąta α za pomocą funkcji trygonometrycznych oraz obliczonych długości krawędzi.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
