Dany jest stożek o promieniu podstawy długości 1 i wysokości ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Wykorzystaj twierdzenie Pitagorasa, żeby obliczyć długość tworzącej stożka:
![]()
![]()
Zauważ, że trójkąt prostokątny złożony z promienia podstawy, tworzącej stożka oraz jego wysokości jest podobny do trójkąta o przyprostokątnej z promienia wpisanej kuli opuszczonej na tworzącą. Oznacz jako 𝑟 promień wpisanej kuli i ułóż odpowiednią proporcję:
![]()
![]()
![]()
Oblicz pole powierzchni kuli:
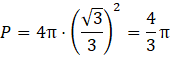
Odp. A. ![]()

Wykorzystaj twierdzenie Pitagorasa, by obliczyć tworzącą stożka. Następnie wykorzystaj podobieństwo trójkątów, by wyznaczyć długość promienia wpisanej kuli. Obliczony promień podstaw do wzoru na pole powierzchni kuli. Przebieg zadania jest podobny jak przykład ze str. 263.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
