Oblicz pole powierzchni oraz objętość stelli octanguli wiedząc, że krawędź tej bryły ma długość 𝑎.
Na ściany figury składa się osiem czworościanów foremnych po trzy (czwarta ściana ukryta) ściany każdy, czyli 24 trójkąty równoboczne. Zatem pole powierzchni jest równe:
![]()
Na objętość stelli octanguli składa się osiem objętości czworościanów foremnych oraz dwa ostrosłupy o podstawie kwadratu. Wysokość tych ostrosłupów możesz obliczyć, wyznaczając odległość przeciwległych krawędzi czworościanu foremnego.
Zaznacz na jednej z krawędzi czworościanu punkt 𝑃 w taki sposób, że dzieli on tę krawędź na dwie równe części. Punkt ten jest spodkiem wysokości dwóch ścian tego czworościanu. Wysokości te, razem z krawędzią czworościanu tworzą trójkąt równoramienny, którego wysokość opuszczona z punktu 𝑃 to szukana odległość.
Wykorzystaj twierdzenie Pitagorasa:
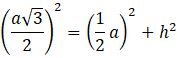
![]()
![]()
To wysokość ostrosłupa. Wykorzystaj ją do obliczenia objętości bryły:
![]()
![]()

Wysokość czworościanu foremnego możesz obliczyć, zauważając, że trójkąt prostokątny złożony z krawędzi bryły oraz ![]()

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
