Dany jest graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej 4. Przeprowadzono przez niego płaszczyznę w taki sposób, że zawiera ona krawędź górnej i dolnej podstawy oraz że kąt dwuścienny między tą płaszczyzną a płaszczyzną podstawy jest równy 30°. Oblicz obwód przekroju bryły utworzonego przez tą płaszczyznę.
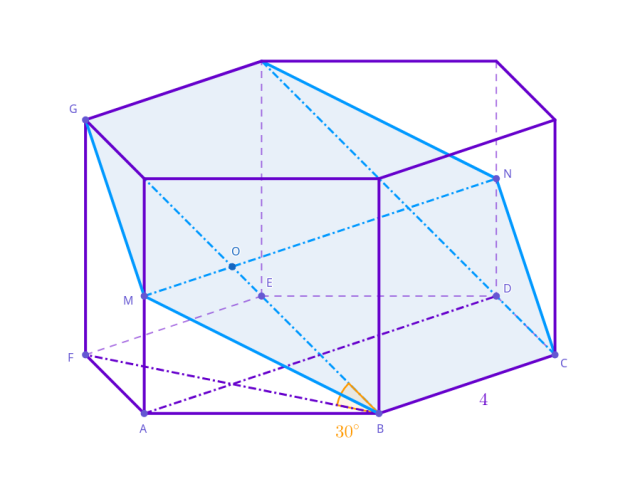
Odcinek 𝐵𝐹 to krótsza przekątna sześciokąta foremnego, czyli ma długość ![]()
![]()
![]()
![]()
Odcinek 𝑀𝑁 ma tą samą długość, co dłuższa przekątna podstawy, czyli 8. Oblicz długość odcinka 𝐵𝐺 za pomocą twierdzenia Pitagorasa:
![]()
![]()
Długość odcinka 𝑀𝑂 jest równa:
![]()
Długość odcinka 𝐵𝑂 to połowa długości odcinka 𝐵𝐺. Oblicz długość odcinka 𝐵𝑀 za pomocą twierdzenia Pitagorasa:
![]()
![]()
Obwód przekroju jest równy:
![]()

Wykorzystaj podany w treści zadaniu kąt, żeby obliczyć wysokość bryły. Oblicz długości przekątnych przekroju. Wykorzystaj fakt, że przekątne te przecinają się pod kątem prostym oraz w charakterystyczny sposób, by obliczyć długość boku przekroju. Zsumuj obliczone długości boków, żeby otrzymać obwód.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
