Dany jest sześcian, w którym poprowadzono przekątną. Następnie z jednego z wierzchołków tego sześcianów prowadzimy prostą przechodzącą przez przekątną pod kątem prostym. Punkt przecięcia się przekątnej oraz tej prostej oznacz 𝑃. Określ stosunek długości odcinków, na jakie punkt 𝑃 dzieli przekątną sześcianu.
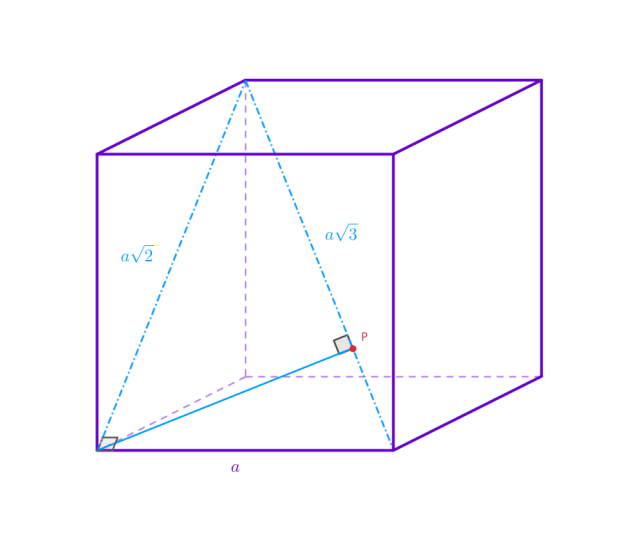
Zauważ, że taka konstrukcja tworzy trójkąt prostokątny o przeciwprostokątnej z przekątnej sześcianu. Punkt 𝑃 jest spodkiem wysokości opuszczonej na tę przeciwprostokątną. Oblicz tę wysokość, licząc pole tego trójkąta na dwa sposoby:
![]()
![]()
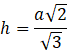
Wykorzystaj fakt, że wysokość opuszczona na przeciwprostokątną w trójkącie prostokątnym dzieli ten trójkąt na trójkąty podobne. Porównaj stosunki odpowiednich długości:
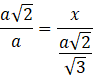
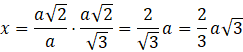
Pozostała część przeciwprostokątnej ma długość:
![]()
Czyli punkt 𝑃 dzieli przekątną sześcianu w stosunku:
![]()

Zauważ, że konstrukcja w sześcianie tworzy trójkąt prostokątny. Wykorzystaj wzór na pole trójkąta, by wyznaczyć wysokość tego trójkąta. Następnie użyj podobieństwa figur, by znaleźć długość jednego z odcinków utworzonego przez punkt 𝑃.

Ćwiczenie A.
252Ćwiczenie B.
253Ćwiczenie C.
253Zadanie 3.
255Zadanie 7.
256Zadanie 8.
256Zadanie 9.
256Zadanie 10.
257Zadanie 11.
257Zadanie 18.
260Zadanie 19.
260Zadanie 23.
261Zadanie 24.
261Zadanie 25.
261Przykład 1.
263Zadanie 1.
264Zadanie 2.
264Zadanie 5.
264Zadanie 6.
265Zadanie 8.
265Zadanie 9.
265Zadanie 10.
265Ćwiczenie A.
267Przykład 3.
273Zadanie 1.
274Zadanie 4.
274Zadanie 7.
274Zadanie 10.
275Zadanie 11.
275Zadanie 12.
275Zadanie 14.
275Zadanie 17.
276Zadanie 1.
281Zadanie 2.
281Zadanie 3.
281Zadanie 4.
282Zadanie 6.
282Zadanie 8.
282Zadanie 10.
283Zadanie 11.
283Zadanie 12.
283Zadanie 13.
283Zadanie 14.
283Zadanie 19.
284Zadanie S1.
284Ćwiczenie B.
286Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 7.
289Zadanie 9.
289Zadanie 14.
290Zadanie 15.
290Zadanie 3.
292Zadanie 5.
292
