![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
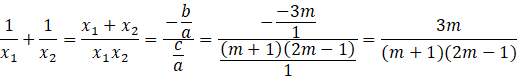
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
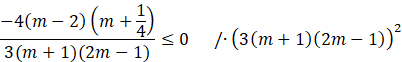
![]()
![]()
![]()
![]()
![]()
ODP:
![]()

Zauważ, że aby równanie miało dwa rozwiązania to
![]() . Oblicz dla jakich
. Oblicz dla jakich
![]() delta będzie większa od zera.
delta będzie większa od zera.
![]()
Skorzystaj ze wzoru skróconego mnożenia na kwadrat różnicy.
![]()
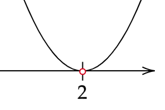
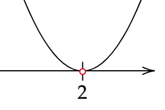
Zauważ, że delta jest większa od zera dla każdej liczby rzeczywistej oprócz 2.
![]()
Oblicz dla jakich
![]() , iloczyn rozwiązań jest różny od zera.
, iloczyn rozwiązań jest różny od zera.
![]()
Skorzystaj z wzorów Viete’a.
![]()
Oblicz deltę i miejsca zerowe powstałego równania.
![]()
![]()
![]()
![]()
Oznacza to, że iloczyn miejsc zerowych jest różny od zera, dla każdej liczby rzeczywistej oprócz
![]() i
i
![]() .
.
![]()
Oblicz dla jakich
![]() spełniona jest nierówność
spełniona jest nierówność
![]() .
.
Zamień sumę ułamków tak, aby uzyskać postać z wzorami Viete’a.
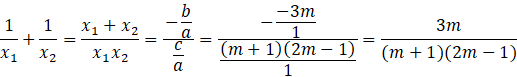
![]()
Oblicz dla jakich
![]() spełnioina jest pierwsza nierówność. Zauważ, że musisz pomnożyć przez kwadrat mianownika, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
spełnioina jest pierwsza nierówność. Zauważ, że musisz pomnożyć przez kwadrat mianownika, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
![]()
![]()
Oblicz dla jakich
![]() nierówność się zeruje.
nierówność się zeruje.
![]()
![]()
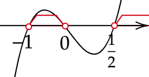
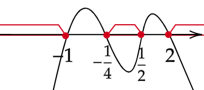
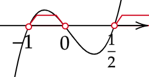
Zaznacz obliczone rozwiązania na osi i zaznacz na niej przedziały, gdy wykres jest nad osią.
![]()
Oblicz dla jakich
![]() spełniona jest druga nierówność. Przenieś wszystko na lewą stronę i odejmij od siebie ułamki.
spełniona jest druga nierówność. Przenieś wszystko na lewą stronę i odejmij od siebie ułamki.
![]()
![]()
![]()
Rozwiąż równanie znajdujące się w liczniku ułamka.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Pomnóż całą nierówność przez kwadrat mianownika, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
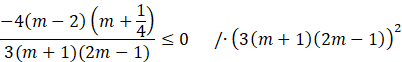
![]()
Oblicz dla jakich
![]() nierówność się zeruje.
nierówność się zeruje.
![]()
![]()
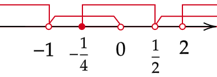
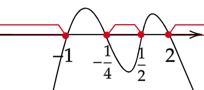
Zaznacz obliczone rozwiązania na osi i zaznacz na niej przedziały, gdy wykres jest pod osią.
![]()
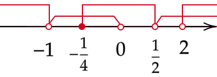
Zaznacz na osi wszystkie obliczone powyżej przedziały. Rozwiązaniem będzie ich część wspólna.
![]()