W tym zadaniu musisz podać pole wycinka kołowego.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
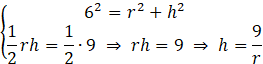
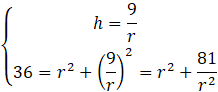
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
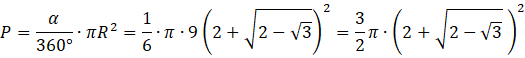

Dzięki znajomości pola trójkąta OAB wyznacz sinus kąta między ramionami za pomocą wzoru ![]()
Kąt między ramionami trójkąta jest równy połowie kąta środkowego, który wyznacza wycinek koła. (jeżeli oznaczysz punkt styczności okręgów przez P otrzymasz 4 kąty, wszystkie będące kątami ostrymi przystających trójkątów prostokątnych, których przyprostokątne są równe promieniowi mniejszego okręgu i odległości od punktu O do punktu styczności z okręgiem, a przeciwprostokątne są równe odległości punktu O i środków mniejszego okręgu)
Oznacz przez h wysokość trójkąta OAB, a przez r promień mniejszego okręgu.
Zapisz równanie wynikające z twierdzenia Pitagorasa dla trójkąta OPB, a także równanie opisujące pole trójkąta OPB. Otrzymasz układ równań z dwoma niewiadomymi.
Rozwiąż układ przez podstawienie za h wielkości zależnej od r, wyznaczonej z drugiego równania. Po podstawieniu h do pierwszego równania otrzymasz ![]()
Aby rozwiązać powyższe równanie, podstaw za r2 zmienną pomocniczą t i rozwiąż równanie kwadratowe pamiętając, że t musi być nieujemne.
Wróć do podstawienia i wyznacz możliwe wartości r. Wynik ![]()
Promień wycinka jest równy sumie odległości punktów O i B oraz promienia okręgu r.
Pole wycinka oblicz korzystając ze wzoru ![]()

Ćwiczenie 1
327Ćwiczenie 2
329Zadanie 1
330Zadanie 2
330Zadanie 3
330Ćwiczenie 1
333Zadanie 1
334Zadanie 2
334Zadanie 3
334Zadanie 1
340Zadanie 5
340Zadanie 6
340Zadanie 7
340Zadanie 8
341Zadanie 18
341Zadanie 19
341Zadanie 1
345Zadanie 2
345Ćwiczenie 6
349Ćwiczenie 7
349Zadanie 1
349Zadanie 3
350Zadanie 4
350Zadanie 5
350Zadanie 6
350Zadanie 10
350Zadanie 11
350Zadanie 12
350Zadanie 13
350Ćwiczenie 2
352Zadanie 1
354Zadanie 2
355Zadanie 3
355Zadanie 4
355Zadanie 5
355Zadanie 6
355Zadanie 7
355Zadanie 8
355Zadanie 3
358Zadanie 7
358Ćwiczenie 2
360Zadanie 5
362Zadanie 6
362Zadanie 16
363Zadanie 17
363Zadanie 11
369Zadanie 13
369Zadanie 14
369Zadanie 18
369Zadanie 19
369Zadanie 20
369Zadanie 21
369Zadanie 22
370Zadanie 24
370Zadanie 30
370
