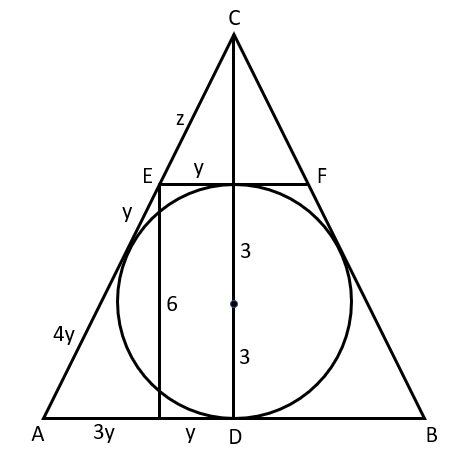
W tym zadaniu musisz podać, ile wynosi obwód trójkąta EFC.
![]()
![]()
![]()
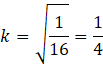
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Korzystając ze znanej zależności między polami trójkąta EFC i trapezu ABFE, a także z tego, że trójkąty ABC i EFC są podobne na mocy cechy kąt – kąt – kąt, wyznacz skalę podobieństwa trójkątów. Następnie do rozwiązania wprowadź przedstawione na rysunku oznaczenia. Poprowadź odcinek równoległy do wysokości trójkąta, przechodzący przez punkt E. Jego długość jest równa dwóm długością promienia. Dla powstałego trójkąta prostokątnego ułóż równanie wynikające z twierdzenia Pitagorasa. Z równania wyznacz y. Następnie ponownie korzystając z podobieństwa trójkątów ABC i EFC wyznacz z. Wykorzystując otrzymane wartości oblicz obwód trójkąta EFC.

Ćwiczenie 1
327Ćwiczenie 2
329Zadanie 1
330Zadanie 2
330Zadanie 3
330Ćwiczenie 1
333Zadanie 1
334Zadanie 2
334Zadanie 3
334Zadanie 1
340Zadanie 5
340Zadanie 6
340Zadanie 7
340Zadanie 8
341Zadanie 18
341Zadanie 19
341Zadanie 1
345Zadanie 2
345Ćwiczenie 6
349Ćwiczenie 7
349Zadanie 1
349Zadanie 3
350Zadanie 4
350Zadanie 5
350Zadanie 6
350Zadanie 10
350Zadanie 11
350Zadanie 12
350Zadanie 13
350Ćwiczenie 2
352Zadanie 1
354Zadanie 2
355Zadanie 3
355Zadanie 4
355Zadanie 5
355Zadanie 6
355Zadanie 7
355Zadanie 8
355Zadanie 3
358Zadanie 7
358Ćwiczenie 2
360Zadanie 5
362Zadanie 6
362Zadanie 16
363Zadanie 17
363Zadanie 11
369Zadanie 13
369Zadanie 14
369Zadanie 18
369Zadanie 19
369Zadanie 20
369Zadanie 21
369Zadanie 22
370Zadanie 24
370Zadanie 30
370
