W tym zadaniu musisz udowodnić twierdzenie.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
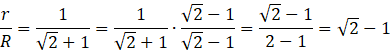
![]()

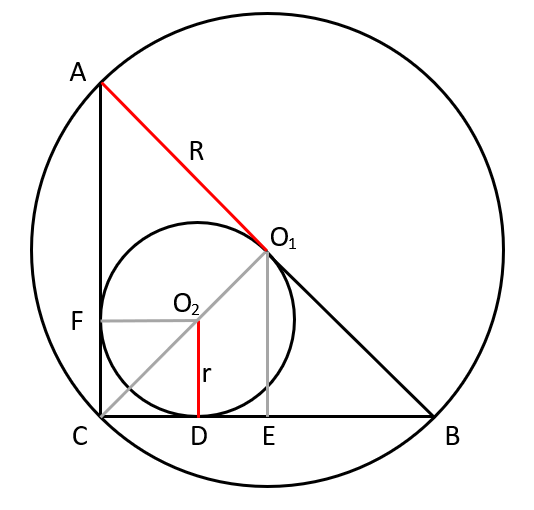
Wyznacz długość przeciwprostokątnej trójkąta równoramiennego korzystając ze wzoru na długość przekątnej kwadratu (trójkąt prostokątny równoramienny jest połową kwadratu). Promień okręgu opisanego na trójkącie prostokątnym jest połową długości przeciwprostokątnej.
Zauważ, że kąty czworokąta CDO2F są proste, a także jego boki są długości r, zatem czworokąt jest kwadratem, o boku długości r i przekątnej długości r![]()
Trójkąt CO1B jest trójkątem prostokątnym równoramiennym o ramionach |CO1| i |O1B|. Odcinek CO1 jest sumą odcinków |CO2| = r![]()
Zapisz ułamek opisujący stosunek pól kół, a następnie skróć ułamek przez ![]()
![]()

Ćwiczenie 1
327Ćwiczenie 2
329Zadanie 1
330Zadanie 2
330Zadanie 3
330Ćwiczenie 1
333Zadanie 1
334Zadanie 2
334Zadanie 3
334Zadanie 1
340Zadanie 5
340Zadanie 6
340Zadanie 7
340Zadanie 8
341Zadanie 18
341Zadanie 19
341Zadanie 1
345Zadanie 2
345Ćwiczenie 6
349Ćwiczenie 7
349Zadanie 1
349Zadanie 3
350Zadanie 4
350Zadanie 5
350Zadanie 6
350Zadanie 10
350Zadanie 11
350Zadanie 12
350Zadanie 13
350Ćwiczenie 2
352Zadanie 1
354Zadanie 2
355Zadanie 3
355Zadanie 4
355Zadanie 5
355Zadanie 6
355Zadanie 7
355Zadanie 8
355Zadanie 3
358Zadanie 7
358Ćwiczenie 2
360Zadanie 5
362Zadanie 6
362Zadanie 16
363Zadanie 17
363Zadanie 11
369Zadanie 13
369Zadanie 14
369Zadanie 18
369Zadanie 19
369Zadanie 20
369Zadanie 21
369Zadanie 22
370Zadanie 24
370Zadanie 30
370
