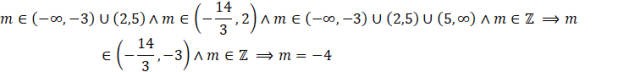1. Największa wartość funkcji:
![]()
2. Dwa miejsca zerowe o takich samych znakach:
2.1.
![]()
2.2.
![]()
3.
![]()
1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.1.
![]()
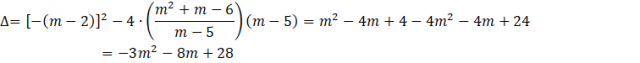
![]()
![]()
![]()
![]()
![]()
![]()
2.2.
![]()
![]()
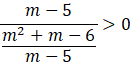
![]()
![]()
![]()
![]()
![]()
![]()
![]()
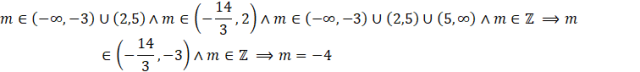
ODP: Warunki podane w treści zadania spełnia
![]()

Zauważ, że aby były spełnione warunki zadania, to musi zachodzić:
1. Aby funkcja osiągała wartość największą, to ramiona paraboli muszą być skierowane do dołu, więc współczynnik kierunkowy musi być ujemny:
![]()
2. Aby równanie miało dwa miejsca zerowe o takich samych znakach, to:
2.1.Delta musi być większa od zera:
![]()
2.2.Iloczyn miejsc zerowych musi być dodatni:
![]()
3. Wartość
![]() , musi być liczbą całkowitą:
, musi być liczbą całkowitą:
![]()
Wyznacz wartości
![]() , dla których spełniony jest pierwszy warunek.
, dla których spełniony jest pierwszy warunek.
1.
![]()
![]()
Wyznacz dziedzinę nierówności, czyli wyklucz
![]() , dla których mianownik zeruję się.
, dla których mianownik zeruję się.
![]()
![]()
Wróć do rozwiązywania powyższej nierówności i pomnóż ją przez
![]() Zauważ, że możesz to zrobić, ponieważ kwadrat jakiejkolwiek liczby jest zawsze dodatni, więc znak nierówności nie zmieni się.
Zauważ, że możesz to zrobić, ponieważ kwadrat jakiejkolwiek liczby jest zawsze dodatni, więc znak nierówności nie zmieni się.
![]()
![]()
Wyznacz rozwiązania pierwszego z nawiasów w powyższej nierówności.
![]()
Oblicz deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
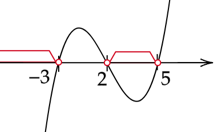
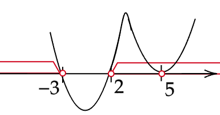
Zaznacz obliczone rozwiązania na osi. Funkcję zacznij rysować od góry, ponieważ współczynnik stojący przy
![]() z największą potęgą jest dodatni. Zaznacz przedziały, gdy wykres jest pod osią.
z największą potęgą jest dodatni. Zaznacz przedziały, gdy wykres jest pod osią.
![]()
Oblicz dla jakich
![]() spełniony jest drugi warunek, czyli delta jest większa od zera i iloczyn miejsc zerowych jest dodatni.
spełniony jest drugi warunek, czyli delta jest większa od zera i iloczyn miejsc zerowych jest dodatni.
2.1.
![]()
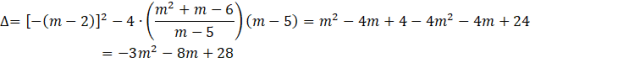
Oblicz deltę z delty i jej miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
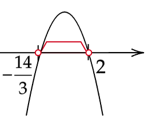
Zaznacz obliczone rozwiązania na osi. Ramiona paraboli skieruj do dołu, ponieważ współczynnik stojący przy
![]() z największą potęgą jest ujemny. Zaznacz przedziały, gdy wykres jest nad osią.
z największą potęgą jest ujemny. Zaznacz przedziały, gdy wykres jest nad osią.
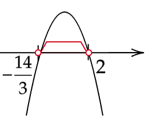
![]()
2.2.
![]()
Zastosuj wzór Viete’a na iloczyn miejsc zerowych.
![]()
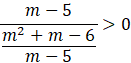
![]()
Wyznacz dziedzinę nierówności, czyli wyklucz
![]() , dla których mianownik zeruję się.
, dla których mianownik zeruję się.
![]()
![]()
Wróć do rozwiązywania powyższej nierówności i pomnóż ją przez
![]() Zauważ, że możesz to zrobić, ponieważ kwadrat jakiejkolwiek liczby jest zawsze dodatni, więc znak nierówności nie zmieni się.
Zauważ, że możesz to zrobić, ponieważ kwadrat jakiejkolwiek liczby jest zawsze dodatni, więc znak nierówności nie zmieni się.
![]()
![]()
![]()
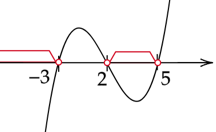
Zaznacz obliczone rozwiązania na osi. Funkcję zacznij rysować od góry, ponieważ współczynnik stojący przy
![]() z największą potęgą jest dodatni. Zaznacz przedziały, gdy wykres jest nad osią.
z największą potęgą jest dodatni. Zaznacz przedziały, gdy wykres jest nad osią.
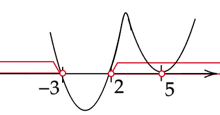
![]()
Zapisz przedział do jakiego należy
![]() , jeśli spełnione są wszystkie powyższe warunki.
, jeśli spełnione są wszystkie powyższe warunki.