Oblicz odległość spodka wysokości ostrosłupa
, którego podstawą jest trapez
od jego krawędzi bocznej
, jeśli przekątna
podstawy ma długość
, jest prostopadła do ramienia
i tworzy z dłuższą podstawą
kąt o mierze
, a każda krawędź boczna tego ostrosłupa ma długość
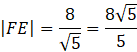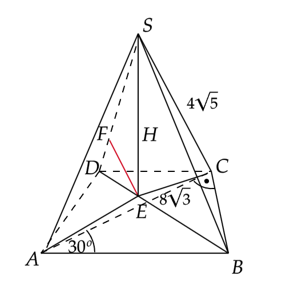
Trójkąty prostokątne AES, BES, CES, DES są przystające z cechy bok – kąt – bok.
Więc
- trapez ABCD jest równoramienny, więc można na nim opisać okrąg.
Trójkąt ABC jest szczególny, bo miary jego kątów wynoszą
Skoro na trapezie ABCD można opisać okrąg, to na trójkącie ABC również.
Trójkąt DES jest prostokątny.
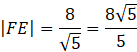
ODP: Odległość spodka wysokości ostrosłupa od jego krawędzi bocznej SD wynosi
Wykonaj rysunek pomocniczy:
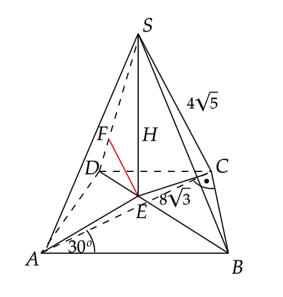
Zauważ, że trójkąty prostokątne AES, BES, CES i DES są przystające z cechy bok – kąt – bok.
Oznacza to, że
, więc trapez ABCD jest równoramienny, czyli można na nim opisać okrąg.
Trójkąt ABC jest szczególny, ponieważ miary jego kątów wynoszą
Oznacza to, że bok leżący naprzeciwko kąta
jest najkrótszy, bok leżący naprzeciwko kąta
jest dłuższy od najkrótszego o
razy, a bok leżący naprzeciwko kąta prostego jest 2 razy dłuższy od najkrótszego. Na tej postawie zapisz długości boków w tym trójkącie.
Skoro na trapezie ABCD można opisać okrąg, to na trójkącie ABC również. Korzystając z własności trójkąta prostokątnego można zauważyć, że promień okręgu opisanego na trójkącie jest równy długości połowy jego przeciwprostokątnej.
Skorzystaj z twierdzenia Pitagorasa w trójkącie prostokątnym ASE i oblicz długość wysokości ostrosłupa.
Zauważ, że trójkąt DES jest prostokątny. Zapisz dwa wzory na obliczenie jego pola.
Pod powyższy wzór podstaw znane wartości i oblicz szukaną długość odcinka.
