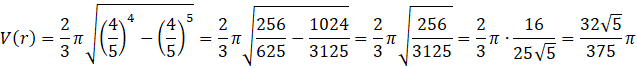![]() – promień podstawy
– promień podstawy
![]() – tworząca stożka
– tworząca stożka
![]() - wysokość
- wysokość
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
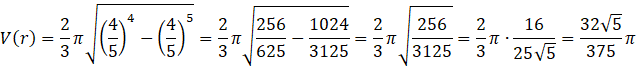
ODP: Największa objętość stożka wynosi
![]() dla promienia równego
dla promienia równego
![]()

Oznacz jako:
![]() – promień podstawy
– promień podstawy
![]() – tworząca stożka
– tworząca stożka
![]() - wysokość
- wysokość
Z treści zadania wiesz, że suma długości tworzącej i promienia wynosi 2. Na tej podstawie wyznacz wartość tworzącej stożka.
![]()
![]()
Zauważ, że obie wielkości, czyli promień i tworząca muszą być większe od zera.
![]()
![]()
![]()
Zapisz dziedzinę równania, czyli przedział spełniający powyższe nierówności.
![]()
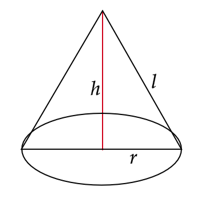
Wykonaj rysunek pomocniczy:
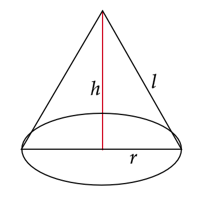
Zauważ, że promień, wysokość i tworząca tworzą trójkąt prostokątny. Skorzystaj z twierdzenia Pitagorasa i wyznacz długość wysokości.
![]()
![]()
![]()
![]()
![]()
Zauważ, że wartość znajdująca się pod pierwiastkiem musi być dodatnia. Wyznacz wartości
![]() spełniające tą własność.
spełniające tą własność.
![]()
![]()
![]()
![]()
Zapisz wzór na objętość stożka.
![]()
Pod powyższe równanie podstaw wyznaczoną wartość
![]() . Zauważ, że powstanie funkcja zmiennej
. Zauważ, że powstanie funkcja zmiennej
![]() Włącz zmienną
Włącz zmienną
![]() pod pierwiastek.
pod pierwiastek.
![]()
Zapisz funkcję pomocniczą zmiennej
![]() . Skorzystaj z wartości pod pierwiastkiem.
. Skorzystaj z wartości pod pierwiastkiem.
![]()
Oblicz pochodną funkcji
![]()
![]()
Oblicz miejsca zerowe powstałej pochodnej, czyli przyrównaj jej wartość do zera.
![]()
Wyłącz
![]() przed nawias.
przed nawias.
![]()
Zauważ, że powstałe równanie składa się z iloczynu dwóch nawiasów. Będzie ono zerem, jeśli chociaż jeden z nich wyzeruję się. Na tej podstawie oblicz rozwiązania każdego z nawiasów.
![]()
![]()
![]()
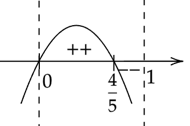
Zaznacz obliczone rozwiązania na osi. Ramiona paraboli skieruj do dołu ponieważ współczynnik stojący przy
![]() z największą potęgą jest ujemny. Pamiętaj o uwzględnieniu dziedziny.
z największą potęgą jest ujemny. Pamiętaj o uwzględnieniu dziedziny.
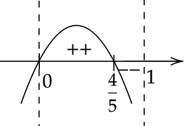
Oznacza to, że pochodna w przedziale
![]() ma jedno miejsce zerowe
ma jedno miejsce zerowe
![]() i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja
i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja
![]() (oraz
(oraz
![]() ) rośnie w przedziale
) rośnie w przedziale
![]() ,a maleje w przedziale
,a maleje w przedziale
![]() . Więc będzie do największa wartość pochodnej.
. Więc będzie do największa wartość pochodnej.
![]()
Oblicz objętość stożka dla największej długości promienia.