Osoba A:
4 + 4 + 4 + 4 + 4 + 4 = 24 – łączna liczba rzutów kostką
Wyznacz medianę parzystej liczby elementów:
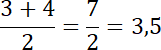
W tym przypadku wyznaczenie dominanty jest niemożliwe, ponieważ każda wartość wypadła 4 – krotnie.
Oblicz średnią arytmetyczną.
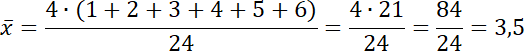
Osoba B:
6 + 5 + 4 + 3 + 2 + 1 = 21 – łączna liczba rzutów kostką
Wyznacz medianę nieparzystej liczby elementów:
2 – wartość środkowa
Najwięcej razy wypadło 1 oczko, więc dominanta jest równa 1.
Oblicz średnią arytmetyczną.
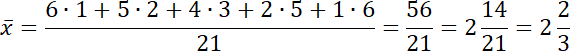
Osoba C:
1 + 2 + 3 + 4 + 5 + 6 = 21 – łączna liczba rzutów kostką
Wyznacz medianę nieparzystej liczby elementów:
5 – wartość środkowa
Najwięcej razy wypadło 6 oczek, więc dominanta jest równa 6.
Oblicz średnią arytmetyczną.
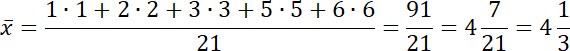
Osoba D:
1 + 3 + 6 + 6 + 3 + 1 = 20 – łączna liczba rzutów kostką
Wyznacz medianę parzystej liczby elementów:
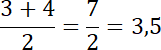
Najwięcej razy wypadły 3 i 4 oczka, więc dominanta jest równa 3 i 4.
Oblicz średnią arytmetyczną.
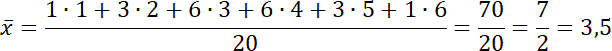
Osoba E:
1 + 2 + 3 + 3 + 2 + 1 = 12 – łączna liczba rzutów kostką
Wyznacz medianę parzystej liczby elementów:
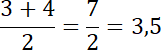
Najwięcej razy wypadły 3 i 4 oczka, więc dominanta jest równa 3 i 4.
Oblicz średnią arytmetyczną.
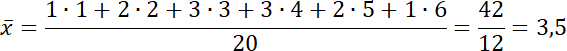
Osoba F:
6 + 3 + 1 + 1 + 3 + 6 = 20 – łączna liczba rzutów kostką
Wyznacz medianę parzystej liczby elementów:
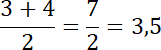
Najwięcej razy wypadło 1 i 6 oczek, więc dominanta jest równa 1 i 6.
Oblicz średnią arytmetyczną.
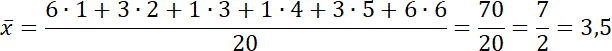

Rozpatrz wyniki każdej osoby: ilość rzutów, jej parzystość, częstość występowania każdego z wyników. Po uzyskaniu tych informacji oblicz medianę, dominantę i średnią arytmetyczną.