Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 26 - strona 14

Wyznacz rozwiązania nierówności $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

ODP: Rozwiązaniem nierówności są $\text{[math]}$ należące do przedziału $\text{[math]}$

$\text{[math]}$

Wyłącz wspólny czynnik przed nawias z lewej strony nierówności.

$\text{[math]}$

Zauważ, że nierówność składa się z iloczynu dwóch równań. Będzie ono zerem, jeśli chociaż jeden z nawiasów będzie zerowy. Przyrównaj więc każdy z nich do zera.

$\text{[math]}$

Oblicz rozwiązania każdego z powstałych równań.

$\text{[math]}$

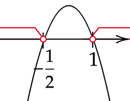
Zaznacz miejsca zerowe na osi, ramiona paraboli skieruj w dół, ponieważ współczynnik przy x z najwyższą potęgą jest ujemny. Zaznacz na niej argumenty, dla których parabola przyjmuje wartości ujemne będzie to rozwiązanie nierówności.

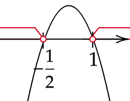
Zapisz uzyskane rozwiązanie.

$\text{[math]}$

Zadanie zamknięte 6, strona 69, Matematyka wokół nas. Klasa 5. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 8., strona 79, Matematyka z plusem. Klasa 3. Podręcznik. Zakres podstawowy – rozwiązania i odpowiedzi

Zadanie 4, strona 206, Matematyka z plusem. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 7., strona 48, Matematyka z kluczem. Klasa 4. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 5., strona 86, Prosto do matury. Klasa 4. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 19., strona 31, Matematyka. Klasa 2. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 1., strona 120, Matematyka. Klasa 2. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 8, strona 207, Matematyka. Klasa 1. Podręcznik. Zakres rozszerzony. Część 1 – rozwiązania i odpowiedzi

Zadanie 8.44., strona 184, Prosto do matury. Klasa 4. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 3., strona 113, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy – rozwiązania i odpowiedzi

2

2

2

2

2

4

4

4

4

4

4

6

6

8

8

8

8

10

10

10

10

10

12

12

12

14

15

16

17

18

19

20

22

24

Pełny spis treści