Udowodnij, że do zbioru wartości funkcji
![]() , dla
, dla
![]() , nie należy żadna liczba całkowita.
, nie należy żadna liczba całkowita.
Założenia:
Dziedziną funkcji f jest zbiór liczb naturalnych.
Teza:
Do zbioru wartości funkcji
![]() nie należy żadna liczba całkowita.
nie należy żadna liczba całkowita.
Dowód:
Oznaczmy dowolną liczbę całkowitą jako:
![]()
Gdyby do zbioru wartości funkcji f należała liczba całkowita k, dla pewnego argumentu
![]() to równanie
to równanie
![]() byłoby prawdziwe. Spróbujmy więc je rozwiązać:
byłoby prawdziwe. Spróbujmy więc je rozwiązać:
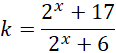
![]()
![]()
![]()
![]()
![]() to liczba parzysta, bo 2 podniesione do dowolnej potęgi naturalnej jest parzyste
to liczba parzysta, bo 2 podniesione do dowolnej potęgi naturalnej jest parzyste
![]() to liczba całkowita, bo różnica dwóch dowolnych liczb całkowitych jest liczbą całkowitą
to liczba całkowita, bo różnica dwóch dowolnych liczb całkowitych jest liczbą całkowitą
![]() to liczba nieparzysta
to liczba nieparzysta
![]() to liczba parzysta, bo dowolna liczba całkowita pomnożona przez liczbę parzystą jest parzysta
to liczba parzysta, bo dowolna liczba całkowita pomnożona przez liczbę parzystą jest parzysta
Zatem po lewej stronie równania mamy liczbę całkowitą pomnożoną przez liczbę parzystą, czyli liczbę parzystą. Po prawej stronie mamy różnicę liczby nieparzystej i liczby parzystej, a więc liczbę nieparzystą. Zatem równanie to jest sprzeczne.
Oznacza to, że żadna liczba całkowita nie może być wartością podanej funkcji, której dziedziną jest liczba naturalna.
Co należało udowodnić.

Na początku zapisz założenia i tezę wyciągnięte z polecenia. Następnie podstaw jako wartość funkcji liczbę całkowitą k i przekształć tak powstałe równanie do momentu aż będzie można zauważyć, że jedna strona równania jest parzysta, a druga nieparzysta. Na końcu stwierdź, że w takim razie równanie to jest sprzeczne i zakończ dowód.

Zadanie 1.6.
204Zadanie 1.7.
205Zadanie 1.8.
205Zadanie 1.9.
205Zadanie 1.10.
205Zadanie 1.11.
205Zadanie 1.12.
205Zadanie 1.13.
206Zadanie 1.14.
206Zadanie 1.15.
206Zadanie Prosto do matury 2
206Zadanie 2.4.
210Zadanie 2.5.
210Zadanie 2.6.
210Zadanie 2.10.
211Zadanie 2.11.
211Zadanie 2.12.
211Zadanie 2.13.
211Zadanie 2.17.
212Zadanie 2.22.
212Zadanie 3.4.
216Zadanie 3.9.
216Zadanie 3.10.
216Zadanie 3.12.
216Zadanie 3.14.
217Zadanie 4.2.
220Zadanie 4.4.
220Zadanie 4.5.
220Zadanie 4.6.
220Zadanie 5.5.
225Zadanie 5.6.
225Zadanie 5.11.
226Zadanie 5.12.
226Zadanie 5.13.
226Zadanie 5.14.
227Zadanie 5.15.
227Zadanie Prosto do matury 5
227Zadanie 6.6.
233Zadanie 6.7.
233Zadanie 6.8.
234Zadanie 6.9.
234Zadanie 6.10.
234Zadanie 6.12.
235Zadanie 6.13.
236Zadanie 6.14.
236Zadanie 6.15.
236Zadanie 6.16.
236Zadanie 6.17.
236Zadanie 6.18.
237Zadanie 7.4.
242Zadanie 7.5.
243Zadanie 7.6.
243Zadanie 7.7.
243Zadanie 7.8.
243Zadanie 7.9.
243Zadanie 7.10.
243Zadanie 7.11.
243Zadanie 7.14.
244Zadanie 7.15.
244Zadanie 7.20.
244Zadanie 7.21.
244Zadanie 8.4.
252Zadanie 8.6.
252Zadanie 8.7.
253Zadanie 8.8.
253Zadanie 8.9.
253Zadanie 8.10.
253Zadanie 8.11.
254Zadanie 8.12.
255Zadanie 8.13.
255Zadanie 8.14.
256Zadanie 8.15.
256Zadanie 8.17.
256Zadanie 8.18.
256Zadanie 9.4.
264Zadanie 9.18.
266Zadanie 9.19.
266Zadanie 9.20.
266Zadanie 9.21.
266Zadanie 9.22.
266Zadanie Prosto do matury 5
267Zadanie 10.4.
271Zadanie 10.5.
272Zadanie 10.6.
272Zadanie 10.11.
274Zadanie 10.12.
274Zadanie 10.13.
274Zadanie 10.16.
275Zadanie Prosto do matury 3.
276Zadanie 11.4.
281Zadanie 11.5.
281Zadanie 11.6.
281Zadanie 11.7.
281Zadanie 11.8.
281Zadanie 11.9.
281Zadanie 11.10.
281Zadanie 11.11.
281Zadanie 11.12.
282Zadanie 11.13.
282Zadanie Prosto do matury 2
282Zadanie 12.4.
288Zadanie 12.5.
288Zadanie 12.6.
288Zadanie 12.7.
289Zadanie 12.8.
289Zadanie 12.9.
289Zadanie 12.11.
290Zadanie 12.12.
290Zadanie 12.13.
290Zadanie 12.20.
290Zadanie 13.3.
300Zadanie 13.5.
300Zadanie 13.6.
300Zadanie 13.7.
300Zadanie 13.8.
300Zadanie 13.12.
301Zadanie Prosto do matury 2
302Zadanie 14.1.
312Zadanie 14.2.
312Zadanie 14.3.
312Zadanie 14.4.
312Zadanie 14.5.
312Zadanie 14.6.
312Zadanie 14.9.
313Zadanie 14.10.
313Zadanie 14.11.
313Zadanie 14.12.
313Zadanie 14.13.
313Zadanie 14.14.
313Zadanie 14.15.
313Zadanie 14.16.
313Zadanie 15.4.
318Zadanie 15.6.
318Zadanie 15.7.
318Zadanie 15.8.
319Zadanie 15.9.
319Zadanie 15.10.
319Zadanie 15.11.
319Zadanie 15.12.
319Zadanie 15.22.
321Zadanie 16.41
328Zadanie 16.42
328Zadanie 16.43
329Zadanie 16.46
329Zadanie 16.48
329Zadanie 16.58
330Zadanie 16.59
330Zadanie 16.63
331Zadanie 16.64
331Zadanie 16.65
331Zadanie 16.68
332
