Dana jest pewna funkcja o podanym zbiorze miejsc zerowych, której dziedziną jest zbiór liczb rzeczywistych. Narysuj przykładowy wykres takiej funkcji.
![]()
Na wykresie miejsca zerowe to argumenty, dla których wykres funkcji przecina oś OX. Aby miejsca zerowe były sumą podanych przedziałów to wykres ten musi leżeć dokładnie na osi OX od argumentu -3 włącznie do argumentu 1 oraz od argumentu 5 aż do dodatniej nieskończoności. Poza tym musi on rozciągać się w nieskończoność wzdłuż osi OX. Ze względu na otwarte nawiasy stosowane przy zapisie tej sumy przedziałów, w odpowiednie miejsca musimy wstawić punkty puste w środku. Narysujmy zatem taki wykres dzieląc go na osobne części.
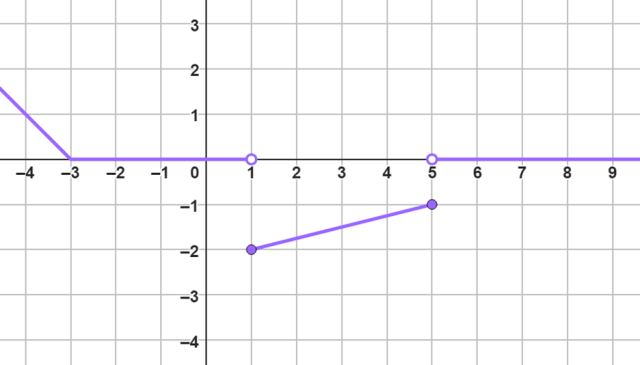

Zauważ, że na wykresie miejsca zerowe to argumenty, dla których wykres funkcji przecina oś OX. Narysuj więc wykres funkcji, który rozciąga się w nieskończoność wzdłuż osi OX i leży dokładnie na niej od argumentu -3 włącznie do argumentu 1 oraz osobno od argumentu 5 aż do dodatniej nieskończoności. Ze względu na stosowane przy zapisie podanej sumy przedziałów nawiasy otwarte musisz w odpowiednie miejsca wstawić punkty puste w środku. Aby było to możliwe bez zmieniania dziedziny funkcji, wystarczy podzielić wykres na kilka osobnych części.

Zadanie 1.6.
204Zadanie 1.7.
205Zadanie 1.8.
205Zadanie 1.9.
205Zadanie 1.10.
205Zadanie 1.11.
205Zadanie 1.12.
205Zadanie 1.13.
206Zadanie 1.14.
206Zadanie 1.15.
206Zadanie Prosto do matury 2
206Zadanie 2.4.
210Zadanie 2.5.
210Zadanie 2.6.
210Zadanie 2.10.
211Zadanie 2.11.
211Zadanie 2.12.
211Zadanie 2.13.
211Zadanie 2.17.
212Zadanie 2.22.
212Zadanie 3.4.
216Zadanie 3.9.
216Zadanie 3.10.
216Zadanie 3.12.
216Zadanie 3.14.
217Zadanie 4.2.
220Zadanie 4.4.
220Zadanie 4.5.
220Zadanie 4.6.
220Zadanie 5.5.
225Zadanie 5.6.
225Zadanie 5.11.
226Zadanie 5.12.
226Zadanie 5.13.
226Zadanie 5.14.
227Zadanie 5.15.
227Zadanie Prosto do matury 5
227Zadanie 6.6.
233Zadanie 6.7.
233Zadanie 6.8.
234Zadanie 6.9.
234Zadanie 6.10.
234Zadanie 6.12.
235Zadanie 6.13.
236Zadanie 6.14.
236Zadanie 6.15.
236Zadanie 6.16.
236Zadanie 6.17.
236Zadanie 6.18.
237Zadanie 7.4.
242Zadanie 7.5.
243Zadanie 7.6.
243Zadanie 7.7.
243Zadanie 7.8.
243Zadanie 7.9.
243Zadanie 7.10.
243Zadanie 7.11.
243Zadanie 7.14.
244Zadanie 7.15.
244Zadanie 7.20.
244Zadanie 7.21.
244Zadanie 8.4.
252Zadanie 8.6.
252Zadanie 8.7.
253Zadanie 8.8.
253Zadanie 8.9.
253Zadanie 8.10.
253Zadanie 8.11.
254Zadanie 8.12.
255Zadanie 8.13.
255Zadanie 8.14.
256Zadanie 8.15.
256Zadanie 8.17.
256Zadanie 8.18.
256Zadanie 9.4.
264Zadanie 9.18.
266Zadanie 9.19.
266Zadanie 9.20.
266Zadanie 9.21.
266Zadanie 9.22.
266Zadanie Prosto do matury 5
267Zadanie 10.4.
271Zadanie 10.5.
272Zadanie 10.6.
272Zadanie 10.11.
274Zadanie 10.12.
274Zadanie 10.13.
274Zadanie 10.16.
275Zadanie Prosto do matury 3.
276Zadanie 11.4.
281Zadanie 11.5.
281Zadanie 11.6.
281Zadanie 11.7.
281Zadanie 11.8.
281Zadanie 11.9.
281Zadanie 11.10.
281Zadanie 11.11.
281Zadanie 11.12.
282Zadanie 11.13.
282Zadanie Prosto do matury 2
282Zadanie 12.4.
288Zadanie 12.5.
288Zadanie 12.6.
288Zadanie 12.7.
289Zadanie 12.8.
289Zadanie 12.9.
289Zadanie 12.11.
290Zadanie 12.12.
290Zadanie 12.13.
290Zadanie 12.20.
290Zadanie 13.3.
300Zadanie 13.5.
300Zadanie 13.6.
300Zadanie 13.7.
300Zadanie 13.8.
300Zadanie 13.12.
301Zadanie Prosto do matury 2
302Zadanie 14.1.
312Zadanie 14.2.
312Zadanie 14.3.
312Zadanie 14.4.
312Zadanie 14.5.
312Zadanie 14.6.
312Zadanie 14.9.
313Zadanie 14.10.
313Zadanie 14.11.
313Zadanie 14.12.
313Zadanie 14.13.
313Zadanie 14.14.
313Zadanie 14.15.
313Zadanie 14.16.
313Zadanie 15.4.
318Zadanie 15.6.
318Zadanie 15.7.
318Zadanie 15.8.
319Zadanie 15.9.
319Zadanie 15.10.
319Zadanie 15.11.
319Zadanie 15.12.
319Zadanie 15.22.
321Zadanie 16.41
328Zadanie 16.42
328Zadanie 16.43
329Zadanie 16.46
329Zadanie 16.48
329Zadanie 16.58
330Zadanie 16.59
330Zadanie 16.63
331Zadanie 16.64
331Zadanie 16.65
331Zadanie 16.68
332
