Przedstaw podaną funkcję w postaci wykresu.
Funkcja, która każdej liczbie naturalnej przyporządkowuje liczbę o 2 większą od niej.
Funkcja ta ma nieskończenie wielką dziedzinę. Dlatego weźmy pod uwagę tylko kilka niewielkich argumentów i obliczmy dla nich wartości tej funkcji. Zauważmy, że tak opisaną funkcję możemy oznaczyć jako f i opisać wzorem:
![]()
Obliczmy jej wartość dla kilku niewielkich argumentów:
![]()
![]()
![]()
![]()
![]()
![]()
Teraz sporządźmy wykres tej funkcji pamiętając, że argumenty zaznaczamy na osi OX, a odpowiadające im wartości na osi OY. Wykres ten będzie obrazował tylko niewielki fragment funkcji, ale w domyśle rozciąga się ona w nieskończoność.
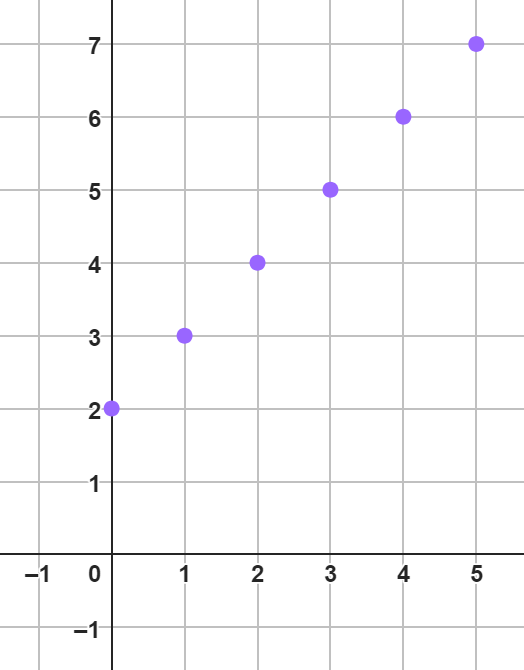

Zauważ, że podana funkcja ma nieskończenie wielką dziedzinę i nie ma sensu próbować wypisywać jej argumentów. W celu skonstruowania jej wykresu weźmy pod uwagę tylko kilka niewielkich argumentów, a w domyśle wykres ten będzie się rozciągał w nieskończoność. Dla tych niewielkich argumentów oblicz wartość funkcji. Dla ułatwienia możesz skonstruować jej wzór, który można odczytać z opisu. Na końcu, po obliczeniu wartości tej funkcji dla niewielkich argumentów, zaznacz je jako punkty w układzie współrzędnych. Pamiętaj, że argumenty zaznaczamy przy pomocy podziałki na osi OX, a odpowiadające im wartości funkcji przy pomocy podziałki na osi OY. Pamiętaj również, aby zaznaczyć wszystkie punkty należące do wykresu tej funkcji jakie są w stanie zmieścić się w narysowanym układzie współrzędnych.

Zadanie 1.6.
204Zadanie 1.7.
205Zadanie 1.8.
205Zadanie 1.9.
205Zadanie 1.10.
205Zadanie 1.11.
205Zadanie 1.12.
205Zadanie 1.13.
206Zadanie 1.14.
206Zadanie 1.15.
206Zadanie Prosto do matury 2
206Zadanie 2.4.
210Zadanie 2.5.
210Zadanie 2.6.
210Zadanie 2.10.
211Zadanie 2.11.
211Zadanie 2.12.
211Zadanie 2.13.
211Zadanie 2.17.
212Zadanie 2.22.
212Zadanie 3.4.
216Zadanie 3.9.
216Zadanie 3.10.
216Zadanie 3.12.
216Zadanie 3.14.
217Zadanie 4.2.
220Zadanie 4.4.
220Zadanie 4.5.
220Zadanie 4.6.
220Zadanie 5.5.
225Zadanie 5.6.
225Zadanie 5.11.
226Zadanie 5.12.
226Zadanie 5.13.
226Zadanie 5.14.
227Zadanie 5.15.
227Zadanie Prosto do matury 5
227Zadanie 6.6.
233Zadanie 6.7.
233Zadanie 6.8.
234Zadanie 6.9.
234Zadanie 6.10.
234Zadanie 6.12.
235Zadanie 6.13.
236Zadanie 6.14.
236Zadanie 6.15.
236Zadanie 6.16.
236Zadanie 6.17.
236Zadanie 6.18.
237Zadanie 7.4.
242Zadanie 7.5.
243Zadanie 7.6.
243Zadanie 7.7.
243Zadanie 7.8.
243Zadanie 7.9.
243Zadanie 7.10.
243Zadanie 7.11.
243Zadanie 7.14.
244Zadanie 7.15.
244Zadanie 7.20.
244Zadanie 7.21.
244Zadanie 8.4.
252Zadanie 8.6.
252Zadanie 8.7.
253Zadanie 8.8.
253Zadanie 8.9.
253Zadanie 8.10.
253Zadanie 8.11.
254Zadanie 8.12.
255Zadanie 8.13.
255Zadanie 8.14.
256Zadanie 8.15.
256Zadanie 8.17.
256Zadanie 8.18.
256Zadanie 9.4.
264Zadanie 9.18.
266Zadanie 9.19.
266Zadanie 9.20.
266Zadanie 9.21.
266Zadanie 9.22.
266Zadanie Prosto do matury 5
267Zadanie 10.4.
271Zadanie 10.5.
272Zadanie 10.6.
272Zadanie 10.11.
274Zadanie 10.12.
274Zadanie 10.13.
274Zadanie 10.16.
275Zadanie Prosto do matury 3.
276Zadanie 11.4.
281Zadanie 11.5.
281Zadanie 11.6.
281Zadanie 11.7.
281Zadanie 11.8.
281Zadanie 11.9.
281Zadanie 11.10.
281Zadanie 11.11.
281Zadanie 11.12.
282Zadanie 11.13.
282Zadanie Prosto do matury 2
282Zadanie 12.4.
288Zadanie 12.5.
288Zadanie 12.6.
288Zadanie 12.7.
289Zadanie 12.8.
289Zadanie 12.9.
289Zadanie 12.11.
290Zadanie 12.12.
290Zadanie 12.13.
290Zadanie 12.20.
290Zadanie 13.3.
300Zadanie 13.5.
300Zadanie 13.6.
300Zadanie 13.7.
300Zadanie 13.8.
300Zadanie 13.12.
301Zadanie Prosto do matury 2
302Zadanie 14.1.
312Zadanie 14.2.
312Zadanie 14.3.
312Zadanie 14.4.
312Zadanie 14.5.
312Zadanie 14.6.
312Zadanie 14.9.
313Zadanie 14.10.
313Zadanie 14.11.
313Zadanie 14.12.
313Zadanie 14.13.
313Zadanie 14.14.
313Zadanie 14.15.
313Zadanie 14.16.
313Zadanie 15.4.
318Zadanie 15.6.
318Zadanie 15.7.
318Zadanie 15.8.
319Zadanie 15.9.
319Zadanie 15.10.
319Zadanie 15.11.
319Zadanie 15.12.
319Zadanie 15.22.
321Zadanie 16.41
328Zadanie 16.42
328Zadanie 16.43
329Zadanie 16.46
329Zadanie 16.48
329Zadanie 16.58
330Zadanie 16.59
330Zadanie 16.63
331Zadanie 16.64
331Zadanie 16.65
331Zadanie 16.68
332
