Korzystając z danych podanych w trójkącie na poniższym rysunku, oblicz wartość długości h z dokładnością do 0,1 cm.
![]()
I wysokość dla h poprowadzoną z kąta o wartości 62°.
![]()
![]()
![]()
![]()
![]()
II wysokość dla h poprowadzoną z kąta o wartości 56°.
![]()
![]()
![]()
![]()
![]()
![]()

Oblicz wartość 3 kąta. Skorzystaj, że suma kątów w dowolnym trójkącie jest równa 180°.
![]()
Czyli trójkąt jest równoramienny, czyli wysokości poprowadzone z kątów, które mają takie same miary są takie same.
I wysokość dla h poprowadzoną z kąta o wartości 62°.
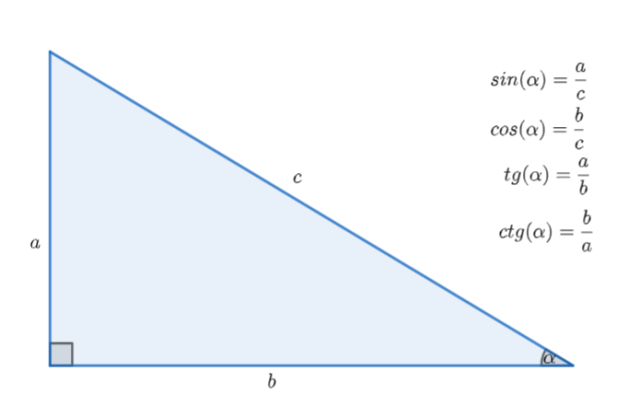
Własności funkcji trygonometrycznych w trójkącie prostokątnym przedstawiają się następująco:
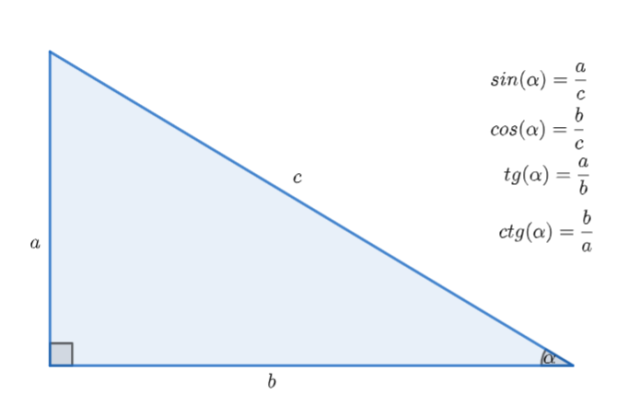
Aby obliczyć h skorzystaj z funkcji ![]()
![]()
![]()
![]()
![]()
![]()
II wysokość dla h poprowadzoną z kąta o wartości 56°.
Trójkąt jest równoramienny, czyli wysokość dzieli podstawę na dwie różne części.
Aby obliczyć h skorzystaj z funkcji ![]()
![]()
![]()
![]()
![]()
![]()
Wysokości w trójkącie:
![]()

Zadanie 8.1.
222Zadanie 8.2.
222Zadanie 8.3.
223Zadanie 8.4.
223Zadanie 8.5.
223Zadanie 8.6.
223Zadanie 8.7.
223Zadanie 8.9.
224Zadanie 8.10.
224Zadanie 8.11.
224Zadanie 8.12.
224Zadanie 8.13.
224Zadanie 8.20.
225Zadanie 8.21.
225Zadanie 8.22.
226Zadanie 8.23.
226Zadanie 8.26.
226Zadanie 8.29.
227Zadanie 8.30.
227Zadanie 8.31.
227Zadanie 8.32.
228Zadanie 8.33.
228Zadanie 8.34.
228Zadanie 8.35.
228Zadanie 8.36.
229Zadanie 8.37.
229Zadanie 8.39.
229Zadanie 8.40.
229Zadanie 8.41.
229Zadanie 8.42.
230Zadanie 8.43.
230Zadanie 8.44.
230Zadanie 8.45.
230Zadanie 8.46.
230Zadanie 8.47.
230Zadanie 8.48.
230Zadanie 8.49.
231Zadanie 8.50.
231Zadanie 8.51.
231Zadanie 8.52.
231Zadanie 8.53.
231Zadanie 8.54.
231Zadanie 8.55.
231Zadanie 8.56.
232Zadanie 8.57.
232Zadanie 8.58.
232Zadanie 8.59.
232Zadanie 8.60.
232Zadanie 16.
234Zadanie 17.
234Zadanie 21.
235Zadanie 24.
235Zadanie 25.
235Zadanie 26.
235Zadanie 27.
235Zadanie 32.
236
