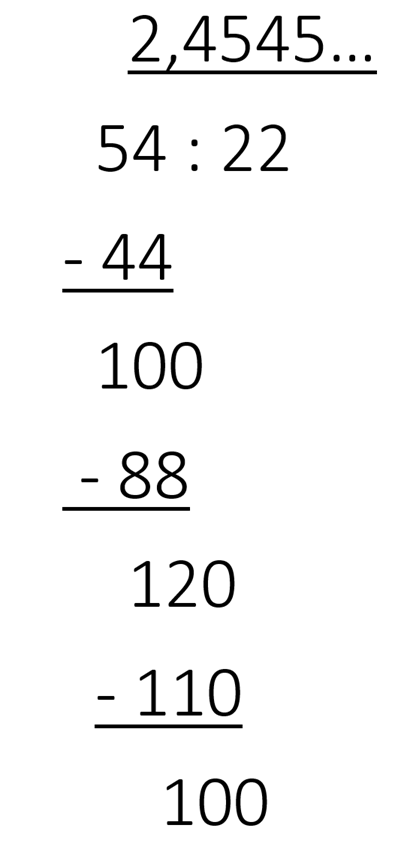
2, 4545… ≈ 2,5
2, 4545… = 2,(45)
Setna cyfra w ułamku okresowym to 5.

Żeby zaokrąglić liczbę 2, 4545… do części dziesiętnych (pierwsza cyfra po przecinku), musisz spojrzeć na części setne (druga cyfra po przecinku). Ponieważ w częściach setnych jest 5, to zaokrąglamy części dziesiętne „w górę”, z 4 do 5.
W celu stworzenia okresu w liczbie 2, 4545… przyjrzyj się, która część się powtarza i weź ją w nawias. W tym przypadku w nawias weź 45, otrzymując 2,(45).
Aby dowiedzieć się, jaka jest setna cyfra po przecinku w tym ułamku okresowym, zauważ, że na nieparzystych miejscach po przecinku zawsze będzie 4, a na parzystych zawsze 5.
[MT1]Grafika do poprawy, nie widać miary dolnego kąta
[MT2] [MT2]Grafika do poprawy, nie widać miary kąta
[MT3] [MT3]Grafika do poprawy, nie widać miary kąta
[MT4] [MT4]Grafika do poprawy, nie widać miary kąta
[MT5] [MT5]Grafika do poprawy, nie widać miary kąta
[MT6] [MT6]Grafika do poprawy, nie widać miary kąta
[MT7] [MT7]Grafika do poprawy, nie widać miary kąta
[MT8]Błędna odpowiedź
[MT9]Jeśli pojawia się podział na inne figury, trzeba by je narysować. Nie ma jednak takiej potrzeby, z rysunku można odczytać podstawę i wysokość trójkąta
[MT10]Jeśli pojawia się podział na inne figury, trzeba by je narysować. Nie ma jednak takiej potrzeby, z rysunku można odczytać podstawę i wysokość równoległoboku
[WS11]Nie rozbijamy na podpunkty, bo każdy wynika z poprzedniego i w osobnych nie będą miały sensu