W tym zadaniu musisz pokazać, korzystając ze wzoru n pole trójkąta, że pole czworokąta wynosi ![]()
Dwie przekątne d1 i d2 dzielą czworokąt na 2 trójkąty prostokątne. Jeśli za a i b oznaczymy fragment przekątnych od ich przecięcia do jednego z narożników, to pole całego czworokąta będzie można obliczyć jako sumę pól tych trójkątów: 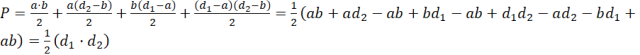
Co należało udowodnić.

Zwróć uwagę na to, jakie trójkąty powstają po podziale czworokąta przez przekątne. Oznacz dowolnymi literami odcinki, które składają się na całą przekątną. Następnie oblicz pole każdego z trójkątów i dodaj je do siebie. Zredukuj wyrazy podobne.

Zadanie 3
100Zadanie 4
100Zadanie 5
100Zadanie 7
101Zadanie 8
101Zadanie 9
101Zadanie 11
102Zadanie 12
102Zadanie dla dociekliwych 3
103Zadanie 7
109Zadanie 8
110Zadanie 9
110Zadanie 10
110Ćwiczenie 1
114Ćwiczenie 3
116Zadanie 1
120Zadanie 2
120Zadanie 4
121Zadanie 9
122Zadanie 10
122Zadanie 11
122Ćwiczenie sprawdzające II
123Ćwiczenie 1
125Ćwiczenie 2
126Ćwiczenie 4
127Zadanie 1
128Zadanie 6
128Zadanie 7
128Ćwiczenie sprawdzające I
129Zadanie 1.1
130Zadanie 1.2
130Zadanie 1.8
130Zadanie 2.7
131
