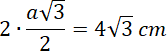
![]()
![]()
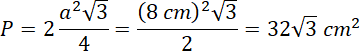
B. Jedna z przekątnych mniejszego czworokąta jest równa 8 cm, C. Pole mniejszego czworokąta jest o 50% mniejsze od pola rombu i D. Otrzymany czworokąt jest wielokątem wypukłym.

W rombie o boku długości 8 cm i kącie ostrym
![]() połączono środki boków i otrzymano czworokąt. W razie potrzeby wykonaj rysunek pomocniczy – narysuj romb o odpowiednich długościach boków i kątach, następnie wyznacz środek każdego boku i połącz te punkty.
połączono środki boków i otrzymano czworokąt. W razie potrzeby wykonaj rysunek pomocniczy – narysuj romb o odpowiednich długościach boków i kątach, następnie wyznacz środek każdego boku i połącz te punkty.
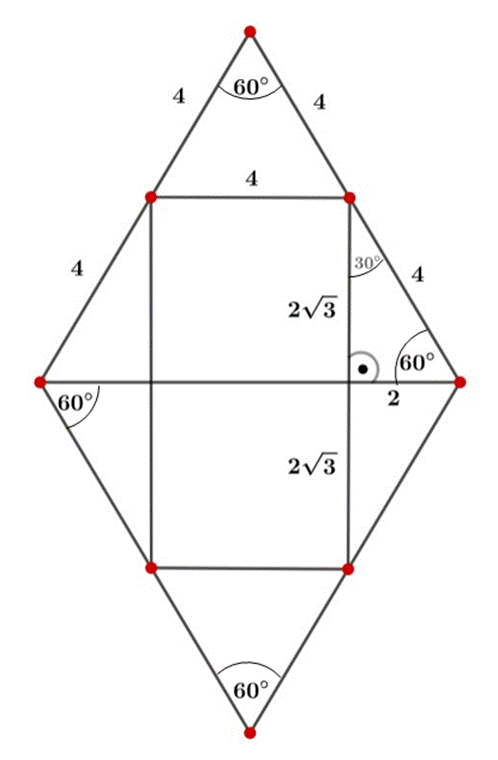
Powstała figura jest równoległobokiem, jedna para boków (przy kącie ostrym rombu) ma 4 cm, gdyż połączone punkty na środkach boków rombu tworzą trójkąt równoboczny o boku 4 cm i kącie
![]() . Długość drugiego boku równoległoboku oblicz, wiedząc, że jest to podwojona wysokość trójkąta
. Długość drugiego boku równoległoboku oblicz, wiedząc, że jest to podwojona wysokość trójkąta
![]() o boku 4 cm. Trójkąt ten możesz wyznaczyć prowadząc wysokość do boku równoległoboku z kąta rozwartego ostrosłupa, który ma miarę
o boku 4 cm. Trójkąt ten możesz wyznaczyć prowadząc wysokość do boku równoległoboku z kąta rozwartego ostrosłupa, który ma miarę
![]() . Wysokość dzieli ten kąt na pół.
. Wysokość dzieli ten kąt na pół.
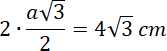
A. Obwód otrzymanego czworokąta jest dwa razy mniejszy od obwodu rombu.
Obwód rombu:
![]()
Obwód równoległoboku:
![]()
Fałsz.
B. Jedna z przekątnych mniejszego czworokąta jest równa 8 cm.
Prawda, a nawet obie – są takie same jak długości boków rombu, gdyż przekątne mniejszego czworokąta są równoległe do boków rombu i ograniczone prostymi zawierającymi boki, obie mają więc 8 cm.
C. Pole mniejszego czworokąta jest o 50% mniejsze od pola rombu.
Jest to prostokąt – równoległobok o przekątnych takich samych długości to prostokąt. Oblicz jego pole:
![]()
Pole rombu oblicz jako pole dwóch trójkątów równobocznych o boku 8 cm:
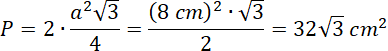
Prawda.
D. Otrzymany czworokąt jest wielokątem wypukłym. Prawda – nie ma w nim kąta wklęsłego.