Na podstawie danych przedstawionych w treści zadania i rysunków oblicz czas, po którym ciężarek uderzy w podłoże, jeśli założymy, że przebywa drogę równą wysokości równi w dwóch przypadkach.
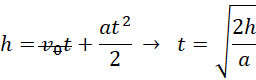
![]()
![]()
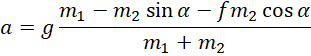
![]()
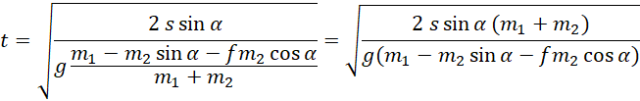
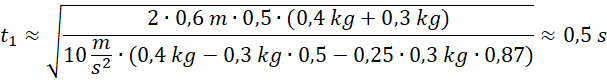
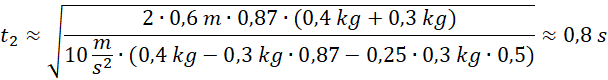

Za pomocą równania ruchu jednostajnie przyspieszonego z zerową prędkością początkową znajdujemy wzór na czas ruchu ciężarka. Aby wyznaczyć przyspieszenie układu, zapisujemy II zasadę dynamiki na kierunku związanym z linką. Wysokość, jaką musi przebyć ciężarek, obliczamy dzięki odpowiedniej funkcji trygonometrycznej. Na koniec łączymy ze sobą wzory i wstawiamy dane liczbowe w dwóch przedstawionych przypadkach.

Zadanie 10.6.
59Zadanie 10.9.
59Zadanie 10.10.
59Zadanie 10.11.
60Zadanie 10.12.
60Zadanie 10.14.
60Zadanie 10.15.
61Zadanie 10.17.
61Zadanie 10.18.
61Zadanie 10.23.
63Zadanie 10.27.
63Zadanie 11.2.
63Zadanie 11.6.
64Zadanie 12.3.
65Zadanie 12.4.
65Zadanie 12.6.
66Zadanie 12.12.
67Zadanie 12.15.
68Zadanie 12.16.
68Zadanie 13.6.
69Zadanie 13.10.
70Zadanie 13.11.
70Zadanie 13.12.
70Zadanie 13.15.
71Zadanie 13.18.
71Zadanie 13.21.
72Zadanie 13.25.
73Zadanie 14.1.
74Zadanie 14.2.
74Zadanie 14.3.
74Zadanie 14.8.
75Zadanie 14.9.
75Zadanie 14.10.
76Zadanie 15.2.
77Zadanie 15.3.
77Zadanie 15.7.
78Zadanie 15.8.
78Zadanie 15.12.
79Zadanie 15.13.
79Zadanie 15.14.
80
