Dane są kąty α i β, dla których zależność ![]()
Niech punkty A = (xa, ya) oraz B = (xb, yb) będą punktami leżącymi na ramionach końcowych kolejno kątów α i β. Z definicji funkcji trygonometrycznych:
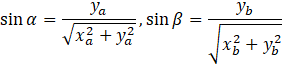
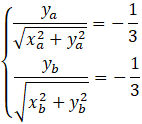
Dla ![]()
![]()
Zatem przykładowy punkt leżący na ramieniu końcowym kąta α ma współrzędne:
![]()
Dla ![]()
![]()
Zatem przykładowy punkt leżący na ramieniu końcowym kąta β ma współrzędne:
![]()
Mając punkty należące do ramion końcowych poszczególnych kątów, pozostaje je narysować:
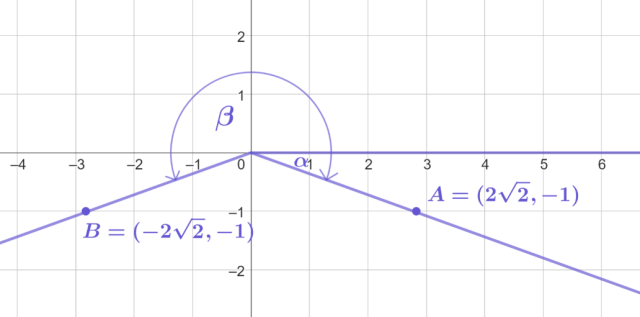

Znajdź współrzędne przykładowych punktów leżących na ramionach końcowych kątów α i β. W tym celu skorzystaj ze wzoru:
![]()
gdzie x i y są współrzędnymi dowolnego punktu P = (x, y) leżącego na końcowym ramieniu kąta α.
Z treści zadania wiadomo, że: ![]()
Ułóż zatem odpowiednie równania i dobierz dowolne wartości liczbowe takie, które je spełniają. Otrzymasz w ten sposób współrzędne punktów leżących na ramionach końcowych poszczególnych kątów. Pamiętaj, aby przy dobieraniu tych liczb sprawdzić, czy po wstawieniu do wzoru na sinus kąta, jego wartość będzie wynosiła ![]()
Narysuj w układzie współrzędnych kąty α i β pamiętając, że wierzchołek kąta umieszczonego w układzie współrzędnych leży w punkcie (0, 0), ramię początkowe pokrywa się z dodatnią częścią osi x, a ramiona końcowe przechodzą przez wyznaczone wcześniej punkty. Kierunek obrotu tych ramion końcowych nie ma w tym przypadku znaczenia, gdyż miary kątów nie zostały podane.

Ćwiczenie B.
146Zadanie 1.
147Zadanie 2.
148Zadanie 3.
148Zadanie 4.
148Zadanie 5.
148Zadanie 6.
148Zadanie 7.
148Ćwiczenie C.
151Zadanie 1.
151Zadanie 2.
151Zadanie 3.
151Zadanie 4.
152Zadanie 5.
152Zadanie 6.
152Zadanie 7.
152Zadanie 8.
152Zadanie 9.
152Ćwiczenie C.
154Zadanie 1.
156Zadanie 2.
156Zadanie 5.
156Zadanie 6.
156Zadanie 7.
157Zadanie 8.
157Zadanie 9.
157Zadanie 10.
157Zadanie 11.
157Zadanie 12.
157Zadanie 13.
157Zadanie 15.
158Zadanie 16.
158Zadanie 1.
160Zadanie 2.
160Zadanie 3.
161Zadanie 4.
161Zadanie 5.
161Zadanie 6.
161Zadanie 7.
161Zadanie 8.
161Zadanie 9.
161Zadanie 10.
161Ćwiczenie B.
164Ćwiczenie C.
165Zadanie 1.
165Zadanie 2.
166Zadanie 4.
166Zadanie 5.
166Zadanie 6.
166Zadanie 7.
166Ćwiczenie A.
168Zadanie 1.
170Zadanie 2.
170Zadanie 3.
170Zadanie 4.
170Zadanie 7.
171Zadanie 8.
171Zadanie 10.
171Zadanie 11.
171Zadanie 1.
174Zadanie 2.
174Zadanie 3.
174Zadanie 4.
174Zadanie 1.
179Zadanie 2.
179Zadanie 3.
179Zadanie 4.
179Zadanie 5.
179Zadanie 6.
180Zadanie 7.
180Zadanie 8.
180Zadanie 9.
180Zadanie 10.
180Zadanie 11.
180Zadanie 12.
180Zadanie 13.
180Zadanie 14.
180Zadanie 15.
180Zadanie 17.
181Zadanie 18.
181Przykład 1.
184Zadanie 1.
184Zadanie 3.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 8.
185Zadanie 9.
185Ćwiczenie B.
187Ćwiczenie C.
187Zadanie 1.
190Zadanie 2.
190Zadanie 3.
191Zadanie 4.
191Zadanie 6.
191Zadanie 7.
191Zadanie 8.
192Zadanie 9.
192Zadanie 10.
192Zadanie 11.
192Zadanie 12.
192Zadanie 13.
192Zadanie 14.
193Zadanie 15.
193Zadanie 16.
193Zadanie 17.
193Zadanie 18.
193Zadanie 1.
196Zadanie 2.
196Zadanie 3.
196Zadanie 5.
197Zadanie 6.
197Zadanie 7.
197Zadanie 8.
197Przykład 1.
200Ćwiczenie C.
202Przykład 7.
205Przykład 8.
206Zadanie 1.
207Zadanie 2.
207Zadanie 3.
207Zadanie 4.
207Zadanie 5.
207Zadanie 6.
207Zadanie 7.
207Zadanie 8.
207Zadanie 9.
207Zadanie 10.
208Zadanie 11.
208Zadanie 12.
208Zadanie 13.
208Zadanie 14.
208Zadanie 15.
208Zadanie 1.
212Zadanie 2.
212Zadanie 3.
212Zadanie 4.
212Zadanie 5.
212Zadanie 6.
212Zadanie 7.
212Zadanie 8.
212Zadanie 9.
213Zadanie 10.
213Zadanie 11.
213Zadanie 12.
213Zadanie 13.
213Zadanie 14.
213Zadanie 1.
214Zadanie 2.
214Zadanie 3.
214Zadanie 6.
214Zadanie 7.
214Zadanie 8.
214Zadanie 11.
214Zadanie 12.
214Zadanie 13.
214Zadanie 14.
214Zadanie 15.
214
