Dane są funkcje: f(x) = sin(x – π), g(x) = -cos x. Wyznacz punkty, w których ich wykresy się przecinają.
Aby wyznaczyć pierwszą współrzędną punktów przecięcia się wykresów obu funkcji, należy rozwiązać równanie:
![]()
![]()
![]()
Wykorzystaj zależność sin(-x) = -sin x:
![]()
![]()
Wykorzystaj wzór redukcyjny sin(π – x) = sin x:
![]()
Rozpatrz dwa przypadki:
I. cos x = 0:
Równanie będzie miało postać:
![]()
Dochodzi do sprzeczności, ponieważ nie istnieje argument, dla którego sinus i cosinus osiągają jednocześnie wartość 0.
II. cos x ≠ 0:
Warunek ten pozwala obustronnie podzielić równanie przez wyrażenie cos x:
![]()
![]()
![]()
![]()
![]()
Rozwiązań tego równania jest nieskończenie wiele, a różnica pomiędzy kolejnymi z nich wynosi π, co wynika z okresowości funkcji tangens. Zatem:
![]()
Aby wyznaczyć drugą współrzędną rozpatrywanych punktów, wstaw otrzymany wynik do wzoru dowolnej z funkcji:
![]()
![]()
Odpowiedź:
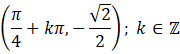

Wyznacz pierwszą współrzędną rozpatrywanych punktów, rozwiązując równanie f(x) = g(x).
Podczas porządkowania równania wykorzystaj zależności:
![]()
![]()
Podczas rozwiązywania równania rozpatrz dwa przypadki: kiedy wyrażenie cos x ma wartość 0 i kiedy jest ono od zera różne. Zauważ, że w pierwszej sytuacji dochodzi do sprzeczności.
Mając wartość pierwszej współrzędnej, wstaw ją do wzoru funkcji f lub g, aby obliczyć drugą. Zapisz odpowiedź.

Ćwiczenie B.
146Zadanie 1.
147Zadanie 2.
148Zadanie 3.
148Zadanie 4.
148Zadanie 5.
148Zadanie 6.
148Zadanie 7.
148Ćwiczenie C.
151Zadanie 1.
151Zadanie 2.
151Zadanie 3.
151Zadanie 4.
152Zadanie 5.
152Zadanie 6.
152Zadanie 7.
152Zadanie 8.
152Zadanie 9.
152Ćwiczenie C.
154Zadanie 1.
156Zadanie 2.
156Zadanie 5.
156Zadanie 6.
156Zadanie 7.
157Zadanie 8.
157Zadanie 9.
157Zadanie 10.
157Zadanie 11.
157Zadanie 12.
157Zadanie 13.
157Zadanie 15.
158Zadanie 16.
158Zadanie 1.
160Zadanie 2.
160Zadanie 3.
161Zadanie 4.
161Zadanie 5.
161Zadanie 6.
161Zadanie 7.
161Zadanie 8.
161Zadanie 9.
161Zadanie 10.
161Ćwiczenie B.
164Ćwiczenie C.
165Zadanie 1.
165Zadanie 2.
166Zadanie 4.
166Zadanie 5.
166Zadanie 6.
166Zadanie 7.
166Ćwiczenie A.
168Zadanie 1.
170Zadanie 2.
170Zadanie 3.
170Zadanie 4.
170Zadanie 7.
171Zadanie 8.
171Zadanie 10.
171Zadanie 11.
171Zadanie 1.
174Zadanie 2.
174Zadanie 3.
174Zadanie 4.
174Zadanie 1.
179Zadanie 2.
179Zadanie 3.
179Zadanie 4.
179Zadanie 5.
179Zadanie 6.
180Zadanie 7.
180Zadanie 8.
180Zadanie 9.
180Zadanie 10.
180Zadanie 11.
180Zadanie 12.
180Zadanie 13.
180Zadanie 14.
180Zadanie 15.
180Zadanie 17.
181Zadanie 18.
181Przykład 1.
184Zadanie 1.
184Zadanie 3.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 8.
185Zadanie 9.
185Ćwiczenie B.
187Ćwiczenie C.
187Zadanie 1.
190Zadanie 2.
190Zadanie 3.
191Zadanie 4.
191Zadanie 6.
191Zadanie 7.
191Zadanie 8.
192Zadanie 9.
192Zadanie 10.
192Zadanie 11.
192Zadanie 12.
192Zadanie 13.
192Zadanie 14.
193Zadanie 15.
193Zadanie 16.
193Zadanie 17.
193Zadanie 18.
193Zadanie 1.
196Zadanie 2.
196Zadanie 3.
196Zadanie 5.
197Zadanie 6.
197Zadanie 7.
197Zadanie 8.
197Przykład 1.
200Ćwiczenie C.
202Przykład 7.
205Przykład 8.
206Zadanie 1.
207Zadanie 2.
207Zadanie 3.
207Zadanie 4.
207Zadanie 5.
207Zadanie 6.
207Zadanie 7.
207Zadanie 8.
207Zadanie 9.
207Zadanie 10.
208Zadanie 11.
208Zadanie 12.
208Zadanie 13.
208Zadanie 14.
208Zadanie 15.
208Zadanie 1.
212Zadanie 2.
212Zadanie 3.
212Zadanie 4.
212Zadanie 5.
212Zadanie 6.
212Zadanie 7.
212Zadanie 8.
212Zadanie 9.
213Zadanie 10.
213Zadanie 11.
213Zadanie 12.
213Zadanie 13.
213Zadanie 14.
213Zadanie 1.
214Zadanie 2.
214Zadanie 3.
214Zadanie 6.
214Zadanie 7.
214Zadanie 8.
214Zadanie 11.
214Zadanie 12.
214Zadanie 13.
214Zadanie 14.
214Zadanie 15.
214
